The energy theorem
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 50
2024-06-29
1237
The energy in a wave is proportional to the square of its amplitude. For a wave of complex shape, the energy in one period will be proportional to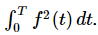 
We can also relate this energy to the Fourier coefficients. We write
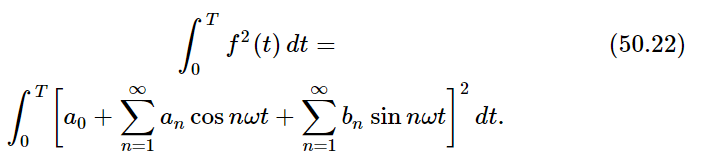
When we expand the square of the bracketed term we will get all possible cross terms, such as a5 cos5ωt⋅a7 cos7ωt and a5 cos5ωt⋅b7 sin7ωt. We have shown above, however, [Eqs. (50.11) and (50.12)] that the integrals of all such terms over one period is zero. We have left only the square terms like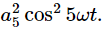 
The integral of any cosine squared or sine squared over one period is equal to T/2, so we get
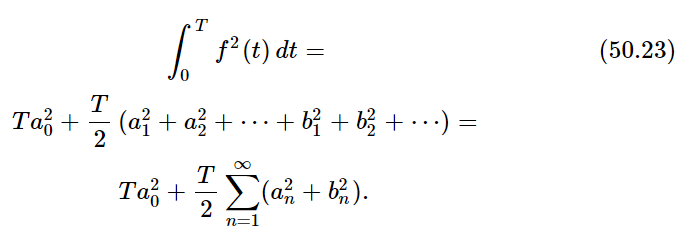
This equation is called the “energy theorem,” and says that the total energy in a wave is just the sum of the energies in all of the Fourier components. For example, applying this theorem to the series (50.19), since [f(t)]2=1 we get
so we learn that the sum of the squares of the reciprocals of the odd integers is π2/8. In a similar way, by first obtaining the Fourier series for the function f(t)=(t−T/2)2 and using the energy theorem, we can prove that 1+1/24+1/34+⋯ is π4/90.
الاكثر قراءة في الصوت
اخر الاخبار
اخبار العتبة العباسية المقدسة
