We now consider another application of the uncertainty relation, Eq. (38.3).

It must not be taken too seriously; the idea is right but the analysis is not very accurate. The idea has to do with the determination of the size of atoms, and the fact that, classically, the electrons would radiate light and spiral in until they settle down right on top of the nucleus. But that cannot be right quantum-mechanically because then we would know where each electron was and how fast it was moving.

Suppose we have a hydrogen atom, and measure the position of the electron; we must not be able to predict exactly where the electron will be, or the momentum spread will then turn out to be infinite. Every time we look at the electron, it is somewhere, but it has an amplitude to be in different places so there is a probability of it being found in different places. These places cannot all be at the nucleus; we shall suppose there is a spread in position of order a. That is, the distance of the electron from the nucleus is usually about a. We shall determine a by minimizing the total energy of the atom.

The spread in momentum is roughly ℏ/a because of the uncertainty relation, so that if we try to measure the momentum of the electron in some manner, such as by scattering x-rays off it and looking for the Doppler effect from a moving scatterer, we would expect not to get zero every time—the electron is not standing still—but the momenta must be of the order p ≈ ℏ/a. Then the kinetic energy is roughly 1/2 mv² = p²/2m = ℏ²/2ma². (In a sense, this is a kind of dimensional analysis to find out in what way the kinetic energy depends upon the reduced Planck constant, upon m, and upon the size of the atom. We need not trust our answer to within factors like 2, π, etc. We have not even defined a very precisely.) Now the potential energy is minus e2 over the distance from the center, say −e²/a, where, we remember, e² is the charge of an electron squared, divided by 4πϵ₀. Now the point is that the potential energy is reduced if a gets smaller, but the smaller a is, the higher the momentum required, because of the uncertainty principle, and therefore the higher the kinetic energy. The total energy is

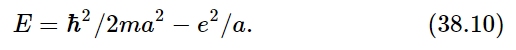
We do not know what a is, but we know that the atom is going to arrange itself to make some kind of compromise so that the energy is as little as possible. In order to minimize E, we differentiate with respect to a, set the derivative equal to zero, and solve for a. The derivative of E is

This particular distance is called the Bohr radius, and we have thus learned that atomic dimensions are of the order of angstroms, which is right: This is pretty good—in fact, it is amazing, since until now we have had no basis for understanding the size of atoms! Atoms are completely impossible from the classical point of view, since the electrons would spiral into the nucleus.

Now if we put the value (38.12) for a₀ into (38.10) to find the energy, it comes out

What does a negative energy mean? It means that the electron has less energy when it is in the atom than when it is free. It means it is bound. It means it takes energy to kick the electron out; it takes energy of the order of 13.6 eV to ionize a hydrogen atom. We have no reason to think that it is not two or three times this—or half of this—or (1/π) times this, because we have used such a sloppy argument. However, we have cheated, we have used all the constants in such a way that it happens to come out the right number! This number, 13.6 electron volts, is called a Rydberg of energy; it is the ionization energy of hydrogen.

So, we now understand why we do not fall through the floor. As we walk, our shoes with their masses of atoms push against the floor with its mass of atoms. In order to squash the atoms closer together, the electrons would be confined to a smaller space and, by the uncertainty principle, their momenta would have to be higher on the average, and that means high energy; the resistance to atomic compression is a quantum-mechanical effect and not a classical effect. Classically, we would expect that if we were to draw all the electrons and protons closer together, the energy would be reduced still further, and the best arrangement of positive and negative charges in classical physics is all on top of each other. This was well known in classical physics and was a puzzle because of the existence of the atom. Of course, the early scientists invented some ways out of the trouble—but never mind, we have the right way out, now! (Maybe.)

Incidentally, although we have no reason to understand it at the moment, in a situation where there are many electrons it turns out that they try to keep away from each other. If one electron is occupying a certain space, then another does not occupy the same space. More precisely, there are two spin cases, so that two can sit on top of each other, one spinning one way and one the other way. But after that we cannot put any more there. We have to put others in another place, and that is the real reason that matter has strength. If we could put all the electrons in the same place, it would condense even more than it does. It is the fact that the electrons cannot all get on top of each other that makes tables and everything else solid.

Obviously, in order to understand the properties of matter, we will have to use quantum mechanics and not be satisfied with classical mechanics.

مواضيع ذات صلة

Energy levels

Bremsstrahlung

Synchrotron radiation

Radiation damping

The rate of radiation of energy

Radiation resistance

شكل جديد للذرة

النموذج الحلزوني التفاعلي- التوليدي للبنية الذرية:

تحليل وتفسير الرؤية الجديدة للبنية الذرية

شكل جديد للذرة في النظرية الحلزونية الكونية: (محاولة بناء نموذج رياضي للذرة)

المتحريان دافيسون وجيرمر يكتشفان موجات الأمير

بور يحل المشكلة باستخدام دستور بلانك – اينشتاين