When a system is oscillating, energy is carried away, and we deduced a formula for the energy which is radiated by an oscillating system. If we know the electric field, then the average of the square of the field times ϵ₀c is the amount of energy that passes per square meter per second through a surface normal to the direction in which the radiation is going:

Any oscillating charge radiates energy; for instance, a driven antenna radiates energy. If the system radiates energy, then in order to account for the conservation of energy we must find that power is being delivered along the wires which lead into the antenna. That is, to the driving circuit the antenna acts like a resistance, or a place where energy can be “lost” (the energy is not really lost, it is really radiated out, but so far as the circuit is concerned, the energy is lost). In an ordinary resistance, the energy which is “lost” passes into heat; in this case the energy which is “lost” goes out into space. But from the standpoint of circuit theory, without considering where the energy goes, the net effect on the circuit is the same—energy is “lost” from that circuit. Therefore, the antenna appears to the generator as having a resistance, even though it may be made with perfectly good copper. In fact, if it is well built it will appear as almost a pure resistance, with very little inductance or capacitance, because we would like to radiate as much energy as possible out of the antenna. This resistance that an antenna shows is called the radiation resistance.

If a current I is going to the antenna, then the average rate at which power is delivered to the antenna is the average of the square of the current times the resistance. The rate at which power is radiated by the antenna is proportional to the square of the current in the antenna, of course, because all the fields are proportional to the currents, and the energy liberated is proportional to the square of the field. The coefficient of proportionality between radiated power and ⟨I²⟩ is the radiation resistance.

An interesting question is, what is this radiation resistance due to? Let us take a simple example: let us say that currents are driven up and down in an antenna. We find that we have to put work in, if the antenna is to radiate energy. If we take a charged body and accelerate it up and down it radiates energy; if it were not charged it would not radiate energy. It is one thing to calculate from the conservation of energy that energy is lost, but another thing to answer the question, against what force are we doing the work? That is an interesting and very difficult question which has never been completely and satisfactorily answered for electrons, although it has been for antennas. What happens is this: in an antenna, the fields produced by the moving charges in one part of the antenna react on the moving charges in another part of the antenna. We can calculate these forces and find out how much work they do, and so find the right rule for the radiation resistance. When we say “We can calculate—” that is not quite right—we cannot, because we have not yet studied the laws of electricity at short distances; only at large distances do we know what the electric field is. We saw the formula (28.3), but at present it is too complicated for us to calculate the fields inside the wave zone. Of course, since conservation of energy is valid, we can calculate the result all right without knowing the fields at short distances. (As a matter of fact, by using this argument backwards it turns out that one can find the formula for the forces at short distances only by knowing the field at very large distances, by using the laws of conservation of energy, but we shall not go into that here.)

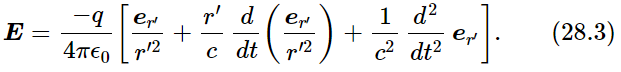
The problem in the case of a single electron is this: if there is only one charge, what can the force act on? It has been proposed, in the old classical theory, that the charge was a little ball, and that one part of the charge acted on the other part. Because of the delay in the action across the tiny electron, the force is not exactly in phase with the motion. That is, if we have the electron standing still, we know that “action equals reaction.” So, the various internal forces are equal, and there is no net force. But if the electron is accelerating, then because of the time delay across it, the force which is acting on the front from the back is not exactly the same as the force on the back from the front, because of the delay in the effect. This delay in the timing makes for a lack of balance, so, as a net effect, the thing holds itself back by its bootstraps! This model of the origin of the resistance to acceleration, the radiation resistance of a moving charge, has run into many difficulties, because our present view of the electron is that it is not a “little ball”; this problem has never been solved. Nevertheless, we can calculate exactly, of course, what the net radiation resistance force must be, i.e., how much loss there must be when we accelerate a charge, in spite of not knowing directly the mechanism of how that force works.

مواضيع ذات صلة

Bremsstrahlung

Synchrotron radiation

Radiation damping

The rate of radiation of energy

شكل جديد للذرة

النموذج الحلزوني التفاعلي- التوليدي للبنية الذرية:

تحليل وتفسير الرؤية الجديدة للبنية الذرية

شكل جديد للذرة في النظرية الحلزونية الكونية: (محاولة بناء نموذج رياضي للذرة)

المتحريان دافيسون وجيرمر يكتشفان موجات الأمير

بور يحل المشكلة باستخدام دستور بلانك – اينشتاين

مشكلة خطوط الأطياف الذرية

رذرفورد يخترع مجموعة شمسية مصغرة