Bernoulli,s Method
المؤلف:
Whittaker, E. T. and Robinson, G.
المصدر:
"A Method of Daniel Bernoulli." §52 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover
الجزء والصفحة:
pp. 98-99
10-12-2021
1544
Bernoulli's Method
In order to find a root of a polynomial equation
 |
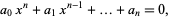(1)
|
consider the difference equation
 |
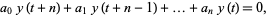(2)
|
which is known to have solution
 |
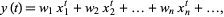(3)
|
where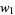 
, 
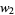, ..., are arbitrary functions of 
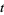with period 1, and 
, ..., 
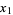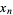are roots of (1). In order to find the absolutely greatest root (1), take any arbitrary values for 
, 
, ..., 
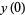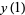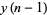. By repeated application of (2), calculate in succession the values 
, 
, 
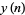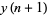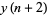, .... Then the ratio of two successive members of this sequence tends in general to a limit, which is the absolutely greatest root of (1).
REFERENCES:
Whittaker, E. T. and Robinson, G. "A Method of Daniel Bernoulli." §52 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 98-99, 1967.
الاكثر قراءة في التحليل العددي
اخر الاخبار
اخبار العتبة العباسية المقدسة
