

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Newton-Cotes Formulas
المؤلف:
Daniell, P. J.
المصدر:
"Remainders in Interpolation and Quadrature Formulae." Math. Gaz. 24
الجزء والصفحة:
...
7-12-2021
1766
Newton-Cotes Formulas
The Newton-Cotes formulas are an extremely useful and straightforward family of numerical integration techniques.
To integrate a function 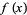 over some interval
over some interval ![[a,b]](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/Inline2.gif) , divide it into
, divide it into 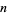 equal parts such that
equal parts such that 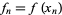 and
and 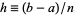 . Then find polynomials which approximate the tabulated function, and integrate them to approximate the area under the curve. To find the fitting polynomials, use Lagrange interpolating polynomials. The resulting formulas are called Newton-Cotes formulas, or quadrature formulas.
. Then find polynomials which approximate the tabulated function, and integrate them to approximate the area under the curve. To find the fitting polynomials, use Lagrange interpolating polynomials. The resulting formulas are called Newton-Cotes formulas, or quadrature formulas.
Newton-Cotes formulas may be "closed" if the interval ![[x_1,x_n]](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/Inline6.gif) is included in the fit, "open" if the points
is included in the fit, "open" if the points ![[x_2,x_(n-1)]](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/Inline7.gif) are used, or a variation of these two. If the formula uses
are used, or a variation of these two. If the formula uses 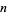 points (closed or open), the coefficients of terms sum to
points (closed or open), the coefficients of terms sum to 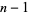 .
.
If the function 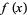 is given explicitly instead of simply being tabulated at the values
is given explicitly instead of simply being tabulated at the values 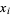 , the best numerical method of integration is called Gaussian quadrature. By picking the intervals at which to sample the function, this procedure produces more accurate approximations (but is significantly more complicated to implement).
, the best numerical method of integration is called Gaussian quadrature. By picking the intervals at which to sample the function, this procedure produces more accurate approximations (but is significantly more complicated to implement).

The 2-point closed Newton-Cotes formula is called the trapezoidal rule because it approximates the area under a curve by a trapezoid with horizontal base and sloped top (connecting the endpoints 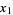 and
and 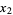 ). If the first point is
). If the first point is 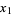 , then the other endpoint will be located at
, then the other endpoint will be located at
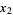 |
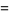 |
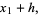 |
(1) |
and the Lagrange interpolating polynomial through the points 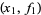 and
and 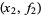 is
is
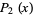 |
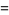 |
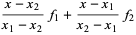 |
(2) |
 |
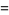 |
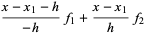 |
(3) |
 |
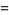 |
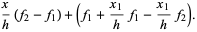 |
(4) |
Integrating over the interval (i.e., finding the area of the trapezoid) then gives
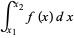 |
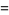 |
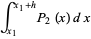 |
(5) |
 |
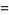 |
![1/(2h)(f_2-f_1)[x^2]_(x_1)^(x_2)+(f_1+(x_1)/hf_1-(x_1)/hf_2)[x]_(x_1)^(x_2)](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/Inline34.gif) |
(6) |
 |
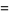 |
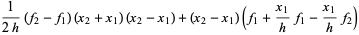 |
(7) |
 |
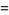 |
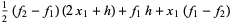 |
(8) |
 |
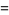 |
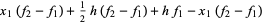 |
(9) |
 |
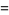 |
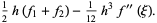 |
(10) |
This is the trapezoidal rule (Ueberhuber 1997, p. 100), with the final term giving the amount of error (which, since 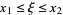 , is no worse than the maximum value of
, is no worse than the maximum value of 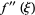 in this range).
in this range).
The 3-point rule is known as Simpson's rule. The abscissas are
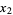 |
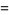 |
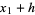 |
(11) |
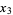 |
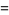 |
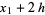 |
(12) |
and the Lagrange interpolating polynomial is
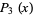 |
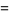 |
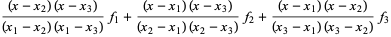 |
(13) |
 |
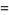 |
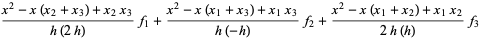 |
(14) |
 |
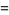 |
(15) |
Integrating and simplifying gives
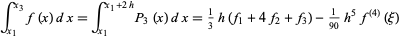 |
(16) |
(Ueberhuber 1997, p. 100).
The 4-point closed rule is Simpson's 3/8 rule,
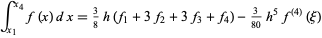 |
(17) |
(Ueberhuber 1997, p. 100). The 5-point closed rule is Boole's rule,
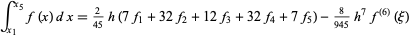 |
(18) |
(Abramowitz and Stegun 1972, p. 886). Higher order rules include the 6-point
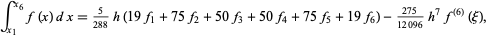 |
(19) |
7-point
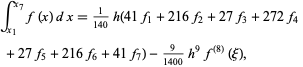 |
(20) |
8-point
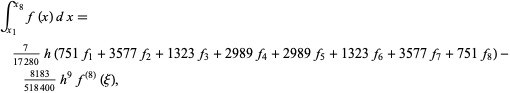 |
(21) |
9-point
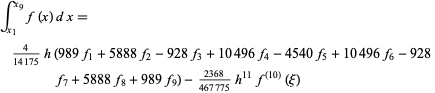 |
(22) |
(Ueberhuber 1997, p. 100), 10-point
![int_(x_1)^(x_(10))f(x)dx=9/(89600)h[2857(f_1+f_(10))+15741(f_2+f_9)+1080(f_3+f_8)+19344(f_4+f_7)+5778(f_5+f_6)]-(173)/(14620)h^(11)f^((10))(xi),](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation8.gif) |
(23) |
and 11-point
![int_(x_1)^(x_(11))f(x)dx=5/(299376)h[16067(f_1+f_(11))+106300(f_2+f_(10))-48525(f_3+f_9)+272400(f_4+f_8)-260550(f_5+f_7)+427368f_6]-(1346350)/(326918592)h^(13)f^((12))(xi)](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation9.gif) |
(24) |
rules.
In general, the 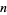 -point rule is given by the analytic expression
-point rule is given by the analytic expression
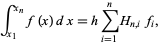 |
(25) |
where
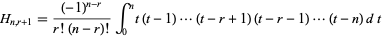 |
(26) |
(Whittaker and Robinson 1967, p. 154). This gives the triangle of coefficients shown in the following table (OEIS A093735 and A093736).
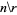 |
0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 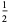 |
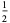 |
||||
| 2 | 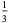 |
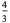 |
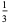 |
|||
| 3 | 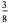 |
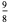 |
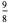 |
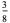 |
||
| 4 | 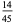 |
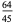 |
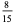 |
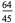 |
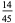 |
|
| 5 | 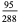 |
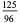 |
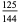 |
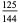 |
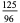 |
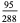 |
Note that
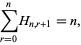 |
(27) |
Closed "extended" rules use multiple copies of lower order closed rules to build up higher order rules. By appropriately tailoring this process, rules with particularly nice properties can be constructed. For 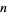 tabulated points, using the trapezoidal rule
tabulated points, using the trapezoidal rule 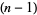 times and adding the results gives
times and adding the results gives
![int_(x_1)^(x_n)f(x)dx=(int_(x_1)^(x_2)+int_(x_2)^(x_3)+...+int_(x_(n-1))^(x_n))f(x)dx
=1/2h[(f_1+f_2)+(f_2+f_3)+...+(f_(n-2)+f_(n-1))+(f_(n-1)+f_n)]
=h(1/2f_1+f_2+f_3+...+f_(n-2)+f_(n-1)+1/2f_n)-1/(12)nh^3f^()(xi)](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation13.gif) |
(28) |
(Ueberhuber 1997, p. 107). Using a series of refinements on the extended trapezoidal rule gives the method known as Romberg integration. A 3-point extended rule for odd 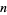 is
is
![int_(x_1)^(x_n)f(x)dx=h[(1/3f_1+4/3f_2+1/3f_3)+(1/3f_3+4/3f_4+1/3f_5)+...+(1/3f_(n-4)+4/3f_(n-3)+1/3f_(n-2))+(1/3f_(n-2)+4/3f_(n-1)+1/3f_n)]
=1/3h(f_1+4f_2+2f_3+4f_4+2f_5+...+4f_(n-1)+f_n)-(n-1)/21/(90)h^5f^((4))(xi).](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation14.gif) |
(29) |
Applying Simpson's 3/8 rule, then Simpson's rule (3-point) twice, and adding gives
![[int_(x_1)^(x_4)+int_(x_4)^(x_6)+int_(x_6)^(x_8)]f(x)dx
=h[(3/8f_1+9/8f_2+9/8f_3+3/8f_4)+(1/3f_4+4/3f_5+1/3f_6)+(1/3f_6+4/3f_7+1/3f_8)]
=h[3/8f_1+9/8f_2+9/8f_3+(3/8+1/3)f_4+4/3f_5+(1/3+1/3)f_6+4/3f_7+1/3f_8]
=h(3/8f_1+9/8f_2+9/8f_3+(17)/(24)f_4+4/3f_5+2/3f_6+4/3f_7+1/3f_8).](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation15.gif) |
(30) |
Taking the next Simpson's 3/8 step then gives
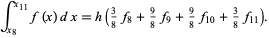 |
(31) |
Combining with the previous result gives
![int_(x_1)^(x_(11))f(x)dx=h[3/8f_1+9/8f_2+9/8f_3+(17)/(24)f_4+4/3f_5+2/3f_6+4/3f_7+(1/3+3/8)f_8+9/8f_9+9/8f_(10)+3/8f_(11)]
=h(3/8f_1+9/8f_2+9/8f_3+(17)/(24)f_4+4/3f_5+2/3f_6+4/3f_7+(17)/(24)f_8+9/8f_9+9/8f_(10)+3/8f_(11)),](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation17.gif) |
(32) |
where terms up to 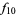 have now been completely determined. Continuing gives
have now been completely determined. Continuing gives
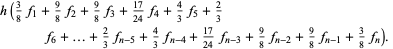 |
(33) |
Now average with the 3-point result
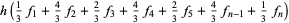 |
(34) |
to obtain
![h[(17)/(48)f_1+(59)/(48)f_2+(43)/(48)f_3+(49)/(48)f_4+(f_5+f_6+...+f_(n-5)+f_(n-4))+(49)/(48)f_(n-3)+(43)/(48)f_(n-2)+(59)/(48)f_(n-1)+(17)/(48)f_n]+O(n^(-4)).](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation20.gif) |
(35) |
Note that all the middle terms now have unity coefficients. Similarly, combining a 3-point with the (2+3)-point rule gives
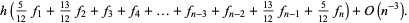 |
(36) |
Other Newton-Cotes rules occasionally encountered include Durand's rule
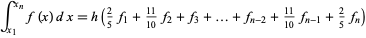 |
(37) |
(Beyer 1987), Hardy's rule
![int_(x_0-3h)^(x_0+3h)f(x)dx=1/(100)h(28f_(-3)+162f_(-2)+22f_0+162f_2+28f_3)
+9/(1400)h^7[2f^((4))(xi_2)-h^2f^((8))(xi_1)],](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation23.gif) |
(38) |
and Weddle's rule
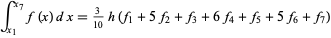 |
(39) |
(Beyer 1987).
The open Newton-Cotes rules use points outside the integration interval, yielding the 1-point
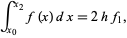 |
(40) |
2-point
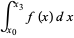 |
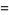 |
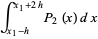 |
(41) |
 |
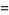 |
![1/(2h)(f_2-f_1)[x^2]_(x_1-h)^(x_1+2h)+(f_1+(x_1)/hf_1-(x_1)/hf_2)[x]_(x_1-h)^(x_1+2h)](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/Inline95.gif) |
(42) |
 |
 |
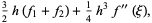 |
(43) |
3-point
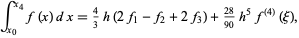 |
(44) |
4-point
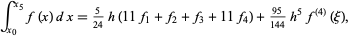 |
(45) |
5-point
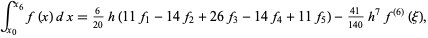 |
(46) |
6-point
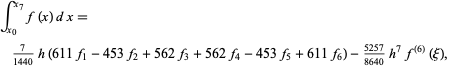 |
(47) |
and 7-point
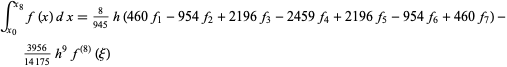 |
(48) |
rules.
A 2-point open extended formula is
![int_(x_1)^(x_n)f(x)dx=h[(1/2f_1+f_2+...+f_(n-1)+1/2f_n)+1/(24)(-f_0+f_2+f_(n-1)-f_(n+1))]+(11(n+1))/(720)h^5f^((4))(xi).](https://mathworld.wolfram.com/images/equations/Newton-CotesFormulas/NumberedEquation31.gif) |
(49) |
Single interval extrapolative rules estimate the integral in an interval based on the points around it. An example of such a rule is
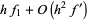 |
(50) |
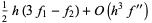 |
(51) |
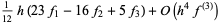 |
(52) |
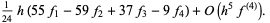 |
(53) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Integration." §25.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 885-887, 1972.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 127, 1987.
Corbit, D. "Numerical Integration: From Trapezoids to RMS: Object-Oriented Numerical Integration." Dr. Dobb's J., No. 252, 117-120, Oct. 1996.
Daniell, P. J. "Remainders in Interpolation and Quadrature Formulae." Math. Gaz. 24, 238, 1940.
Fornberg, B. "Calculation of Weights in Finite Difference Formulas." SIAM Rev. 40, 685-691, 1998.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 160-161, 1956.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Classical Formulas for Equally Spaced Abscissas." §4.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 124-130, 1992.
Sloane, N. J. A. Sequences A093735 and A093736 in "The On-Line Encyclopedia of Integer Sequences."
Ueberhuber, C. W. Numerical Computation 2: Methods, Software, and Analysis. Berlin: Springer-Verlag, 1997.
Whittaker, E. T. and Robinson, G. "The Newton-Cotes Formulae of Integration." §76 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 152-156, 1967.
 الاكثر قراءة في التحليل العددي
الاكثر قراءة في التحليل العددي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















