x

هدف البحث
بحث في العناوين
بحث في المحتوى
بحث في اسماء الكتب
بحث في اسماء المؤلفين

اختر القسم
موافق


تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Separation Axioms
المؤلف:
Alexandroff, P. and Hopf, H
المصدر:
Topologie, Vol. 1. New York: Chelsea 1972.
الجزء والصفحة:
...
28-7-2021
2142
A list of five properties of a topological space 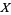 expressing how rich the "population" of open sets is. More precisely, each of them tells us how tightly a closed subset can be wrapped in an open set. The measure of tightness is the extent to which this envelope can separate the subset from other subsets. The numbering from 0 to 4 refers to an increasing degree of separation.
expressing how rich the "population" of open sets is. More precisely, each of them tells us how tightly a closed subset can be wrapped in an open set. The measure of tightness is the extent to which this envelope can separate the subset from other subsets. The numbering from 0 to 4 refers to an increasing degree of separation.
0. T0-separation axiom: For any two points 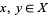 , there is an open set
, there is an open set 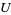 such that
such that 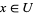 and
and 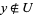 or
or 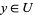 and
and 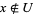 .
.
1. T1-separation axiom: For any two points 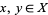 there exists two open sets
there exists two open sets 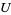 and
and 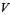 such that
such that 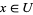 and
and 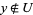 , and
, and 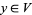 and
and 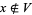 .
.
2. T2-separation axiom: For any two points 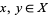 there exists two open sets
there exists two open sets 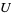 and
and 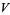 such that
such that 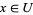 ,
, 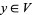 , and
, and 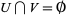 .
.
3. T3-separation axiom: 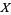 fulfils
fulfils 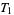 and is regular.
and is regular.
4. T4-separation axiom: 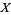 fulfils
fulfils 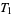 and is normal.
and is normal.
Some authors (e.g., Cullen 1968, pp. 113 and 118) interchange axiom 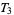 and regularity, and axiom
and regularity, and axiom 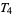 and normality.
and normality.
A topological space fulfilling 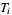 is called a
is called a 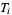 -space for short. In the terminology of Alexandroff and Hopf (1972),
-space for short. In the terminology of Alexandroff and Hopf (1972), 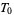 -spaces are also called Kolmogorov spaces,
-spaces are also called Kolmogorov spaces, 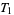 -spaces are Fréchet spaces,
-spaces are Fréchet spaces, 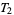 -spaces are Hausdorff spaces,
-spaces are Hausdorff spaces, 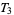 -spaces are Vietoris spaces, and
-spaces are Vietoris spaces, and 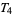 -spaces are Tietze spaces. These names can also be referred to the topologies.
-spaces are Tietze spaces. These names can also be referred to the topologies.
A topological space fulfilling one of the axioms also fulfils all preceding axioms, since 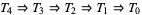 . None of these implications can be reversed in general. This is possible only under additional assumptions. For example, a regular
. None of these implications can be reversed in general. This is possible only under additional assumptions. For example, a regular 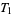 -space is
-space is 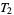 , and a compact
, and a compact 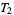 -space is
-space is 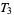 (McCarty 1967, p. 145). A metric topology is always
(McCarty 1967, p. 145). A metric topology is always 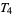 , whereas the trivial topology on a space with at least two elements is not even
, whereas the trivial topology on a space with at least two elements is not even 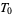 . An example of a topology that is
. An example of a topology that is 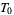 but not
but not 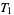 is the one whose open sets are the intervals
is the one whose open sets are the intervals 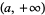 of the real line. Given two distinct real numbers
of the real line. Given two distinct real numbers 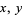 , if
, if 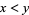 , then
, then 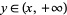 , but
, but 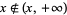 . This shows that axiom
. This shows that axiom 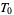 is fulfilled. Axiom
is fulfilled. Axiom 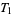 is not, since it can be easily shown that
is not, since it can be easily shown that 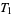 is true iff all singleton sets are closed. For this reason, the Zariski topology of
is true iff all singleton sets are closed. For this reason, the Zariski topology of 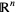 is
is 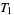 . However, it is not
. However, it is not 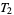 , because the intersection of two open sets is always nonempty.
, because the intersection of two open sets is always nonempty.
Note that in this context the word axiom is not used in the meaning of "principle" of a theory, which has necessarily to be assumed, but in the meaning of "requirement" contained in a definition, which can be fulfilled or not, depending on the cases.
REFERENCES:
Alexandroff, P. and Hopf, H. Topologie, Vol. 1. New York: Chelsea 1972.
Cullen, H. F. "Separation Axioms." Ch. 3 in Introduction to General Topology. Boston, MA: Heath, pp. 99-140, 1968.
Joshi, K. D. "Separation Axioms." Ch. 7 in Introduction to General Topology. New Delhi, India: Wiley, pp. 159-188, 1983.
McCarty, G. Topology, an Introduction with Application to Topological Groups. New York: McGraw-Hill, 1967.
Willard, S. "The Separation Axioms." §13 in General Topology. Reading, MA: Addison-Wesley, pp. 85-92, 1970.