A set 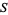 is discrete in a larger topological space  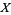if every point  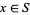has a neighborhood  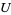such that {x}" src="https://mathworld.wolfram.com/images/equations/DiscreteSet/Inline5.gif" style="height:15px; width:71px" />. The points of 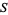 are then said to be isolated (Krantz 1999, p. 63). Typically, a discrete set is either finite or countably infinite. For example, the set of integers is discrete on the real line. Another example of an infinite discrete set is the set {1/n for all integers n>1}" src="https://mathworld.wolfram.com/images/equations/DiscreteSet/Inline7.gif" style="height:15px; width:147px" />. On any reasonable space, a finite set is discrete. A set is discrete if it has the discrete topology, that is, if every subset is open.

In the case of a subset 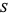, as in the examples above, one uses the relative topology on 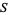. Sometimes a discrete set is also closed. Then there cannot be any accumulation points of a discrete set. On a compact set such as the sphere, a closed discrete set must be finite because of this.

REFERENCES:

Krantz, S. G. "Discrete Sets and Isolated Points." §4.6.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 63-64, 1999.