A convex function is a continuous function whose value at the midpoint of every interval in its domain does not exceed the arithmetic mean of its values at the ends of the interval.

More generally, a function 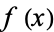 is convex on an interval  if for any two points 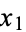 and  in  and any  where ,

(Rudin 1976, p. 101; cf. Gradshteyn and Ryzhik 2000, p. 1132).

If  has a second derivative in , then a necessary and sufficient condition for it to be convex on that interval is that the second derivative 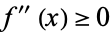 for all  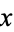in .

If the inequality above is strict for all  and , then  is called strictly convex.

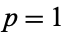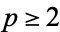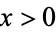Examples of convex functions include  for  or even ,  for , and 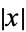 for all 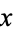. If the sign of the inequality is reversed, the function is called concave.

REFERENCES:

Eggleton, R. B. and Guy, R. K. "Catalan Strikes Again! How Likely is a Function to be Convex?" Math. Mag. 61, 211-219, 1988.

Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1132, 2000.

Rudin, W. Principles of Mathematical Analysis, 3rd ed. New York: McGraw-Hill, 1976.

Webster, R. Convexity. Oxford, England: Oxford University Press, 1995.

اخر الاخبار

اخبار العتبة العباسية المقدسة

مجموعة العميد التربوية تعقد اجتماعًا لمناقشة الاستعدادات الخاصة بالموسم التدريبي الصيفي

قسم الإعلام ينظم ورشة تدريبية حول تطبيق (إعلامي) لعدد من منتسبي قسم حفظ النظام

قسم الشؤون الخدمية ينفذ حملة لتنظيف الشوارع المحيطة بصحن مرقد أبي الفضل العباس (عليه السلام)

وفد العتبة العباسية المقدسة يزور شعبة الإعداد البدني للاطّلاع على برنامج تأهيل المنتسبين الجدد

المزيد

الآخبار الصحية

ماذا يحدث إذا تناولنا الطعام مرة واحدة فقط في اليوم

اكتشاف عوامل خطر غير متوقعة لمرض الكبد الدهني

فيروس هانتا والسفينة الموبوءة.. تحديث من الصحة العالمية

طبيب يحسم الجدل السجائر الإلكترونية وعلاقتها بالسرطان

المزيد

الآخبار التكنلوجية

لأول مرة في الولايات المتحدة.. تشغيل مفاعل مصغر نووي يغذي الذكاء الاصطناعي بالطاقة

الكشف عن تفاصيل أول عملية ناجحة لاستعادة انتاج الحيوانات المنوية

أطلس يكشف خفايا الجسم البشري بدقة أرفع بـ50 مرة من شعر الإنسان

المتحف المصري الكبير يتحول إلى "أيقونة خضراء" بدعم ياباني

المزيد