Baire's category theorem, also known as Baire's theorem and the category theorem, is a result in analysis and set theory which roughly states that in certain spaces, the intersection of any countable collection of "large" sets remains "large." The appearance of "category" in the name refers to the interplay of the theorem with the notions of sets of first and second category.

Precisely stated, the theorem says that if a space 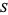 is either a complete metric space or a locally compact T2-space, then the intersection of every countable collection of dense open subsets of  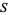is necessarily dense in .

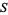The above-mentioned interplay with first and second category sets can be summarized by a single corollary, namely that spaces 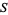 that are either complete metric spaces or locally compact Hausdorff spaces are of second category in themselves. To see that this follows from the above-stated theorem, let  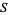be either a complete metric space or a locally compact Hausdorff space and note that if {E_i}={E_i}_(i in N)" src="https://mathworld.wolfram.com/images/equations/BaireCategoryTheorem/Inline6.gif" style="height:17px; width:80px" /> is a countable collection of nowhere dense subsets of 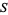 and if  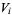denotes the complement in  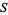of the closure  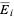of 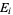, then each set  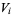is necessarily dense in 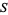. Because of the theorem, it follows that the intersection of all the sets  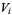must be nonempty (and indeed must be dense in 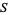), thereby proving that  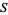cannot be written as the union of the sets 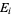. In particular, such spaces  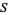cannot be written as the countable union of sets which are nowhere dense in themselves and are therefore second category sets relative to themselves.

REFERENCES:

Rudin, W. Functional Analysis. New York: McGraw-Hill, 1991.