A vector bundle is special class of fiber bundle in which the fiber is a vector space 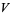. Technically, a little more is required; namely, if  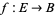is a bundle with fiber 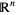, to be a vector bundle, all of the fibers  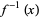for 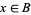 need to have a coherent vector space structure. One way to say this is that the "trivializations" 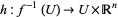, are fiber-for-fiber vector space isomorphisms.

A vector bundle is a total space 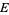 along with a surjective map  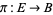to a base manifold 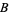. Any fiber  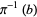is a vector space isomorphic to .

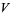The simplest nontrivial vector bundle is a line bundle on the circle, and is analogous to the Möbius strip.

One use for vector bundles is a generalization of vector functions. For instance, the tangent vectors of an 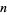-dimensional manifold are isomorphic to  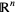at a point  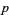in a coordinate chart. But the isomorphism with  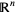depends on the choice of coordinate chart. Nearby 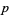, the vector fields look like functions. To define vector fields on the whole manifold requires the tangent bundle, which is a special case of a vector bundle.

A bundle section of a vector bundle 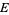 is a map  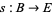whose projection,  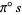is the identity map on 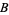. For instance, on a trivial bundle 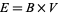, a section  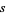corresponds to a function  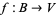by .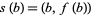

Near every point in a vector bundle, there is a trivialization. The structure of the vector bundle, as in all bundles, is that it is locally trivial. In the case of a vector bundle, the transition functions between the trivializations take values in linear invertible transformations of the fiber.

Since the element zero in 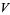 is fixed by any linear transformation, the zero section always exists. By "nontrivial section," it is meant that it is not the zero section.

There are several adjectives that can specify properties of a vector bundle. A complex vector bundle has a fiber 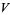 that is a complex vector space. A real vector bundle has a fiber that is a real vector space, which is the default kind of vector bundle. A line bundle has a fiber that is one dimensional.

A continuous vector bundle is a manifold 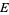 with a continuous projection map 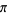. A smooth vector bundle is a smooth manifold  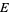with a smooth projection 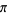. Finally, a holomorphic vector bundle is a complex manifold  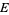with a holomorphic projection 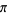. In this last case, the fiber must be a complex vector space. So there could be a smooth complex vector bundle, but not a holomorphic real vector bundle.

Vector bundles can have metrics on their fibers, either Riemannian or Hermitian, and vector bundle connections.