Roughly speaking, a tangent vector is an infinitesimal displacement at a specific point on a manifold. The set of tangent vectors at a point 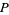 forms a vector space called the tangent space at 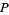, and the collection of tangent spaces on a manifold forms a vector bundle called the tangent bundle.

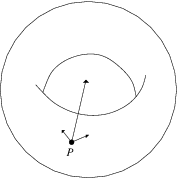
A tangent vector at a point 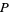 on a manifold is a tangent vector at  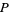in a coordinate chart. A change in coordinates near  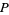causes an invertible linear map of the tangent vector's representations in the coordinates. This transformation is given by the Jacobian, which must be nonsingular in a change of coordinates. Hence the tangent vectors at  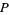are well-defined. A vector field is an assignment of a tangent vector for each point. The collection of tangent vectors forms the tangent bundle, and a vector field is a section of this bundle.

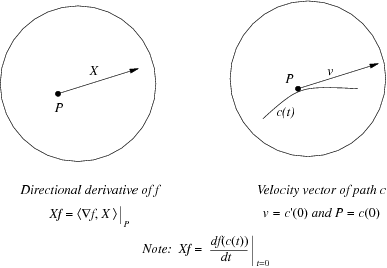
Tangent vectors are used to do calculus on manifolds. Since manifolds are locally Euclidean, the usual notions of differentiation and integration make sense in any coordinate chart, and they can be carried over to manifolds. More specifically, a tangent vector is the manifold version of a directional derivative (at a point). An alternative analogy with calculus is the related notion of a velocity vector.

There are at least three different points of view on tangent vectors. Each has its own pluses and minuses. The extrinsic points of view use the vector space structure of Euclidean space. Thinking of a manifold as a submanifold of Euclidean space, a tangent vector can be thought of as an element in a tangent plane, or submanifold tangent space. In a coordinate chart, a tangent vector is a vector in a (chart) chart tangent space, which is just a copy of Euclidean space.

The problem with the extrinsic points of view is that they depend on a choice of embedding or coordinate chart. There are a couple of ways to think about a tangent vector intrinsically, as an element of an abstract intrinsic tangent space. These are more satisfying from an abstract point of view, but sometimes it is necessary to do calculations in coordinate charts.

It is important to distinguish tangent vectors at 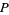 from tangent vectors at any other point 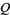, although they may seem parallel. On a Lie group, there is a notion of parallelism, and there exist nonvanishing vector fields. In general, this is far from being true. On the sphere 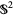, for instance, any smooth vector field must vanish somewhere.

A more intrinsic geometric definition of a tangent vector is to take a tangent vector at 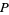 to be an equivalence class of paths through  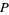which agree to first order. An extrinsic geometric definition, for a submanifold, is to view the tangent vectors as a subspace of the tangent vectors of the ambient space,

Algebraically, a vector field on a manifold is a derivation on the ring of smooth functions. That is, a vector field acts on smooth functions and satisfies the product rule. A vector field 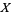 acts on a function by the directional derivative on the function,

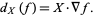(1)

It is more precise to say that the tangent bundle is the topological sheaf of derivations on the sheaf of smooth functions, in which case the tangent vectors at 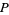 are in the stalk of the sheaf at .

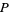In fact, in coordinates 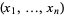, the notation for the standard basis of tangent vectors at 0 is

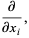(2)

where the derivation 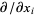 of 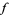 is the usual partial derivative

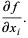(3)

Letting the base point vary in the coordinate chart, 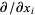 are vector fields, but are only defined in this coordinate chart.