A fiber bundle (also called simply a bundle) with fiber 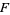 is a map  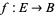where 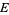 is called the total space of the fiber bundle and  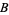the base space of the fiber bundle. The main condition for the map to be a fiber bundle is that every point in the base space  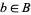has a neighborhood  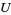such that  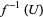is homeomorphic to  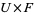in a special way. Namely, if

is the homeomorphism, then

where the map 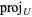 means projection onto the  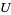component. The homeomorphisms  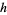which "commute with projection" are called local trivializations for the fiber bundle 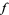. In other words,  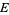looks like the product  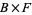(at least locally), except that the fibers  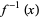for 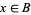 may be a bit "twisted."

A fiber bundle is the most general kind of bundle. Special cases are often described by replacing the word "fiber" with a word that describes the fiber being used, e.g., vector bundles and principal bundles.

Examples of fiber bundles include any product 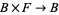 (which is a bundle over  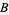with fiber 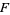), the Möbius strip (which is a fiber bundle over the circle with fiber given by the unit interval [0,1]; i.e., the base space is the circle), and  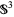(which is a bundle over  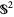with fiber 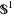). A special class of fiber bundle is the vector bundle, in which the fiber is a vector space.

Some of the properties of graphs of functions 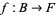 carry over to fiber bundles. A graph of such a function sits in  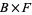as 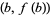. A graph always projects onto the base  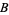and is one-to-one.

A fiber bundle 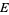 is a total space and, like 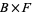, it has a projection 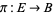. The preimage, 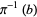, of any point  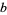is isomorphic to 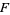. Unlike 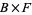, there is no canonical projection from  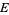to 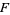. Instead, maps to  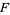only make sense locally on 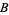. Near any point  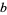in the base 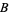, there is a trivialization of  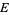in which there are actual functions from a neighborhood to .

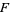These local functions can sometimes be patched together to give a (global) section 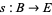 such that the projection of  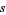is the identity. This is analogous to the map from a domain  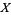of a function  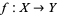to its graph in  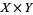by .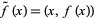

A fiber bundle also comes with a group action on the fiber. This group action represents the different ways the fiber can be viewed as equivalent. For instance, in topology, the group might be the group of homeomorphisms of the fiber. The group on a vector bundle is the group of invertible linear maps, which reflects the equivalent descriptions of a vector space using different vector bases.

Fiber bundles are not always used to generalize functions. Sometimes they are convenient descriptions of interesting manifolds. A common example in geometric topology is a torus bundle on the circle.