A class formed by sets in 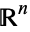 which have essentially the same structure, regardless of size, shape and dimension. The "essential structure" is what a set keeps when it is transformed by compressing or dilating its parts, but without cutting or gluing. The most important feature that is preserved is the system of internal closed paths. In particular, the fundamental group remains unchanged. This object, however, only characterizes the loops, i.e., the paths which are essentially circular lines, whereas the homotopy type also refers to higher dimensional closed paths, which correspond to the boundaries of 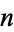-spheres. Hence the homotopy type yields a more precise classification of geometric objects. As for the circular paths, it makes no difference whether the object is located in the plane or on the surface of a sphere, so the fundamental group is the same in both cases.

The homotopy type, however, is different, since the plane does not contain any spherical path. In general, two closed paths in a set are compared by verifying if they can be reduced to the same geometric object in the set. A circular path on a surface can be reduced to any given point of the same surface by first contracting it to its center and the moving the center to the given point. The same is true for a spherical path in a solid. All closed paths in a square and in a cube are of the same kind as a point, hence a cube, a square and a point are of the same homotopy type.

In more general cases, however, holes and gaps can be obstructions to the transformations described above. A hollow sphere can be contracted to a spherical surface, but there is no way to reduce it further. The case of the cube, the square and the point shows that a homotopy type can include sets of different dimensions: hence its elements are not all homeomorphic, but are related in a more general way. According to the formal definition, two sets 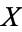 and 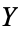 are of the same homotopy type if one can find two continuous maps  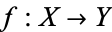and 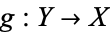 such that the map compositions  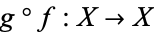and 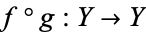 not necessarily are equal to the identity maps on  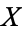and 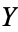 respectively, but are homotopic to them, i.e., they can be reduced to them by continuous deformations.