Negative Binomial Distribution
المؤلف:
Beyer, W. H
المصدر:
CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press
الجزء والصفحة:
...
19-4-2021
2157
Negative Binomial Distribution
The negative binomial distribution, also known as the Pascal distribution or Pólya distribution, gives the probability of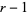 
successes and 
failures in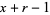 
trials, and success on the 
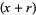th trial. The probability density function is therefore given by
where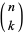 
is a binomial coefficient. The distribution function is then given by
where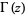 
is the gamma function, 
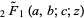is a regularized hypergeometric function, and 
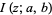is a regularized beta function.
The negative binomial distribution is implemented in the Wolfram Language as NegativeBinomialDistribution[r, p].
Defining
the characteristic function is given by
 |
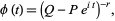(9)
|
and the moment-generating function by
 |
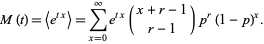(10)
|
Since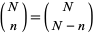 
,
The raw moments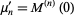 
are therefore
where
 |
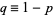(19)
|
and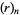 
is the Pochhammer symbol. (Note that Beyer 1987, p. 487, apparently gives the mean incorrectly.)
This gives the central moments as
The mean, variance, skewness and kurtosis excess are then
which can also be written
The first cumulant is
 |
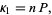(31)
|
and subsequent cumulants are given by the recurrence relation
 |
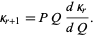(32)
|
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 533, 1987.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 118, 1992.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
