Let there be 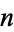 ways for a "good" selection and  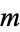ways for a "bad" selection out of a total of  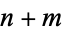possibilities. Take  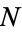samples and let  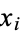equal 1 if selection  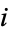is successful and 0 if it is not. Let  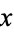be the total number of successful selections,

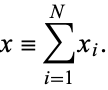(1)

The probability of 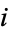 successful selections is then

			(2)
			(3)
			(4)

The hypergeometric distribution is implemented in the Wolfram Language as HypergeometricDistribution[N, n, m+n].

The problem of finding the probability of such a picking problem is sometimes called the "urn problem," since it asks for the probability that 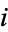 out of  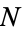balls drawn are "good" from an urn that contains  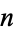"good" balls and  "bad" balls. It therefore also describes the probability of obtaining exactly 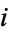 correct balls in a pick- 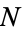lottery from a reservoir of  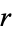balls (of which  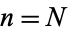are "good" and  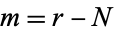are "bad"). For example, for  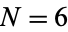and 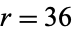, the probabilities of obtaining  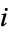correct balls are given in the following table.

number correct	probability	odds
0	0.3048	2.280:1
1	0.4390	1.278:1
2	0.2110	3.738:1
3	0.04169	22.99:1
4	0.003350	297.5:1
5		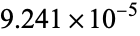10820:1
6

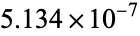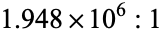The 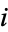th selection has an equal likelihood of being in any trial, so the fraction of acceptable selection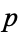s  is

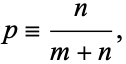(5)

i.e.,

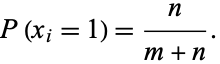(6)

The expectation value of 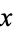 is therefore simply

			(7)
			(8)
			(9)
			(10)

This can also be computed by direct summation as

			(11)
			(12)

The variance is

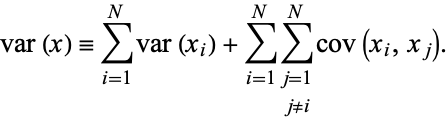(13)

Since 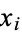 is a Bernoulli variable,

			(14)
			(15)
			(16)
			(17)
			(18)

so

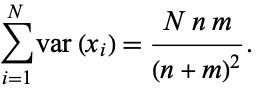(19)

For 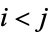, the covariance is

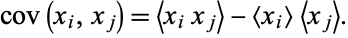(20)

The probability that both 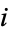 and 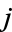 are successful for  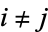is

			(21)
			(22)
			(23)

But since 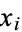 and 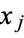 are random Bernoulli variables (each 0 or 1), their product is also a Bernoulli variable. In order for  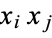to be 1, both  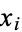and 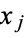 must be 1,

			(24)
			(25)
			(26)

Combining (26) with

			(27)
			(28)

gives

			(29)
			(30)

There are a total of 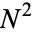 terms in a double summation over 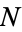. Howeve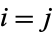r,  for 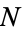 of these, so there are a total of  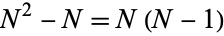terms in the covariance summation

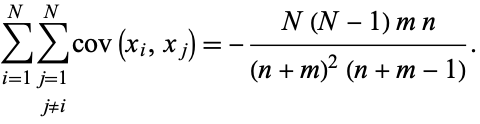(31)

Combining equations (◇), (◇), (◇), and (◇) gives the variance

			(32)
			(33)

so the final result is

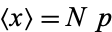(34)

and, since

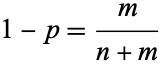(35)

and

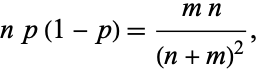(36)

we have

			(37)
			(38)
			(39)

This can also be computed directly from the sum

			(40)
			(41)

The skewness is

			(42)
			(43)

and the kurtosis excess is given by a complicated expression.

The generating function is

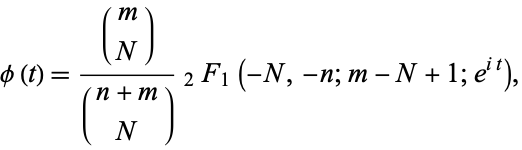(44)

where 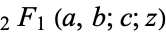 is the hypergeometric function.

If the hypergeometric distribution is written

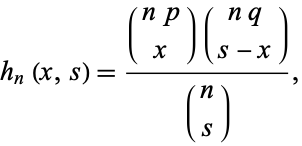(45)

then

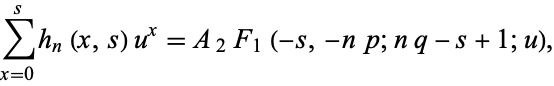(46)

where 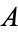 is a constant.

REFERENCES:

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 532-533, 1987.

Feller, W. "The Hypergeometric Series." §2.6 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 41-45, 1968.

Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 113-114, 1992.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد