1

المرجع الالكتروني للمعلوماتية

الرياضيات

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي

الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية

الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق

الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات

الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل

المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات

التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات

علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان

الرياضيات : الاحتمالات و الاحصاء :

Rayleigh Distribution

المؤلف:  Papoulis, A

المصدر:  Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill

الجزء والصفحة:  pp. 104 and 148

13-4-2021

2372

Rayleigh Distribution

RayleighDistribution

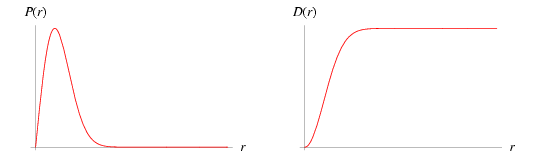
The distribution with probability density function and distribution function

P(r) = (re^(-r^2/(2s^2)))/(s^2)

(1)
D(r) = 1-e^(-r^2/(2s^2))

(2)

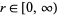for r in [0,infty) and parameter s.

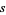It is implemented in the Wolfram Language as RayleighDistribution[s].

The raw moments are given by

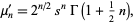(3)

where 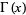Gamma(x) is the gamma function, giving the first few as

= 1

(4)
= ssqrt(pi/2)

(5)
= 2s^2

(6)
= 3s^3sqrt(pi/2)

(7)
= 8s^4.

(8)

The central moments are therefore

mu_2 = (4-pi)/2s^2

(9)
mu_3 = sqrt(pi/2)(pi-3)s^3

(10)
mu_4 = (32-3pi^2)/4s^4.

(11)

The mean, variance, skewness, and kurtosis excess are

mu = ssqrt(pi/2)

(12)
sigma^2 = (4-pi)/2s^2

(13)
gamma_1 = (2(pi-3)sqrt(pi))/((4-pi)^(3/2))

(14)
gamma_2 = -(6pi^2-24pi+16)/((pi-4)^2).

(15)

The characteristic function is

phi(t)=1-sqrt(pi/2)ste^(-s^2t^2/2)[erfi((st)/(sqrt(2)))-i].

(16)

REFERENCES:

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 104 and 148, 1984.

EN

تصفح الموقع بالشكل العمودي