Amazingly, the distribution of a sum of two normally distributed independent variates 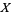 and 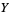 with means and variances  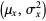and 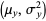, respectively is another normal distribution

(1)

which has mean

(2)

and variance

(3)

By induction, analogous results hold for the sum of 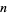 normally distributed variates.

An alternate derivation proceeds by noting that

		{[phi(t)]^n}(x)" src="https://mathworld.wolfram.com/images/equations/NormalSumDistribution/Inline8.gif" style="height:19px; width:94px" />	(4)
			(5)

where 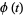 is the characteristic function and  is the inverse Fourier transform, taken with parameters .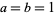

More generally, if  is normally distributed with mean 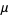 and variance 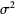, then a linear function of ,

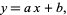(6)

is also normally distributed. The new distribution has mean 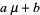 and variance 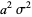, as can be derived using the moment-generating function

			(7)
			(8)
			(9)
			(10)
			(11)

which is of the standard form with

			(12)
			(13)

For a weighted sum of independent variables

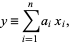(14)

the expectation is given by

			(15)
			(16)
			(17)
			(18)
			(19)

Setting this equal to

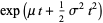(20)

gives

			(21)
			(22)

Therefore, the mean and variance of the weighted sums of 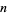 random variables are their weighted sums.

If 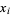 are independent and normally distributed with mean 0 and variance 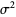, define

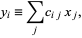(23)

where 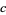 obeys the orthogonality condition

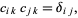(24)

with 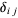 the Kronecker delta. Then  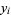are also independent and normally distributed with mean 0 and variance .

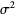Cramer showed the converse of this result in 1936, namely that if 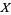 and 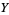 are independent variates and  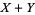has a normal distribution, then both  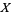and 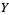 must be normal. This result is known as Cramer's theorem.