Normal Distribution Function

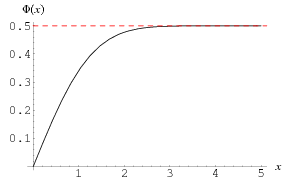
A normalized form of the cumulative normal distribution function giving the probability that a variate assumes a value in the range ,

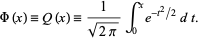(1)

It is related to the probability integral

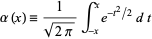(2)

by

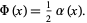(3)

Let 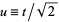 so 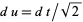. Then

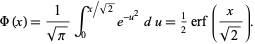(4)

Here, erf is a function sometimes called the error function. The probability that a normal variate assumes a value in the range  is therefore given by

(5)

Neither  nor erf can be expressed in terms of finite additions, subtractions, multiplications, and root extractions, and so must be either computed numerically or otherwise approximated.

Note that a function different from 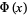 is sometimes defined as "the" normal distribution function

			(6)
			(7)
			(8)
			(9)

(Feller 1968; Beyer 1987, p. 551), although this function is less widely encountered than the usual 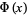. The notation  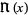is due to Feller (1971).

The value of 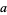 for which  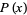falls within the interval  with a given probability 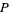 is a related quantity called the confidence interval.

For small values 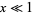, a good approximation to  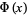is obtained from the Maclaurin series for erf,

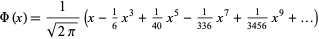(10)

(OEIS A014481). For large values 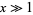, a good approximation is obtained from the asymptotic series for erf,

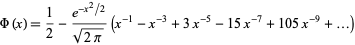(11)

(OEIS A001147).

The value of 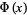 for intermediate  can be computed using the continued fraction identity

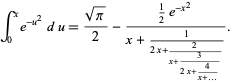(12)

A simple approximation of 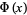 which is good to two decimal places is given by

{0.1x(4.4-x) for 0<=x<=2.2; 0.49 for 2.2<x<2.6; 0.50 for x>=2.6. " src="https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/NumberedEquation9.gif" style="height:62px; width:247px" />

(13)

Abramowitz and Stegun (1972) and Johnson et al. (1994) give other functional approximations. An approximation due to Bagby (1995) is

{1-1/(30)[7e^(-x^2/2)+16e^(-x^2(2-sqrt(2)))+(7+1/4pix^2)e^(-x^2)]}^(1/2). " src="https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/NumberedEquation10.gif" style="height:34px; width:389px" />

(14)

The plots below show the differences between 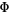 and the two approximations.

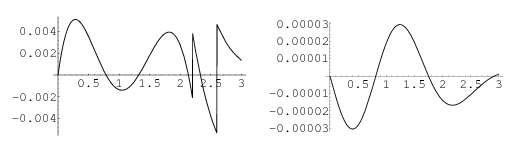
The value of 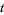 giving  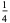is known as the probable error of a normally distributed variate.

---

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 931-933, 1972.

Bagby, R. J. "Calculating Normal Probabilities." Amer. Math. Monthly 102, 46-49, 1995.

Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.

Bryc, W. "A Uniform Approximation to the Right Normal Tail Integral." Math. Comput. 127, 365-374, 2002.

Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.

Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, p. 45, 1971.

Hastings, C. Approximations for Digital Computers. Princeton, NJ: Princeton University Press, 1955.

Johnson, N.; Kotz, S.; and Balakrishnan, N. Continuous Univariate Distributions, Vol. 1, 2nd ed. Boston, MA: Houghton Mifflin, 1994.

Patel, J. K. and Read, C. B. Handbook of the Normal Distribution. New York: Dekker, 1982.

Sloane, N. J. A. Sequences A001147/M3002 and A014481 in "The On-Line Encyclopedia of Integer Sequences."

Whittaker, E. T. and Robinson, G. "Normal Frequency Distribution." Ch. 8 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 164-208, 1967.

مواضيع ذات صلة

Trial

Sampling

Sample Proportion

Sample

Poisson Trials

Experiment

Wiener Numbers

Time Series Analysis

Spencer,s Formula

Redundancy

Predictability

Moving Average