Cauchy Distribution
المؤلف:
Papoulis, A.
المصدر:
Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill
الجزء والصفحة:
...
3-4-2021
2505
Cauchy Distribution
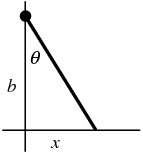
The Cauchy distribution, also called the Lorentzian distribution or Lorentz distribution, is a continuous distribution describing resonance behavior. It also describes the distribution of horizontal distances at which a line segment tilted at a random angle cuts the x-axis.
Let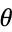 
represent the angle that a line, with fixed point of rotation, makes with the vertical axis, as shown above. Then
so the distribution of angle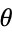 
is given by
 |
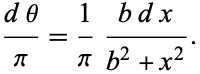(5)
|
This is normalized over all angles, since
 |
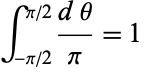(6)
|
and
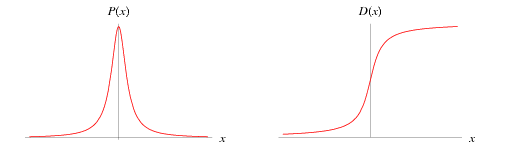
The general Cauchy distribution and its cumulative distribution can be written as
where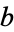 
is the half width at half maximum and 
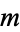is the statistical median. In the illustration about, 
.
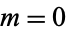The Cauchy distribution is implemented in the Wolfram Language as CauchyDistribution[m, Gamma/2].
The characteristic function is
The moments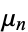 
of the distribution are undefined since the integrals
 |
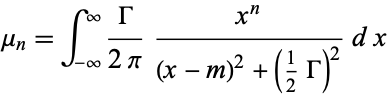(14)
|
diverge for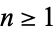 
.
If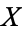 
and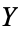 
are variates with a normal distribution, then 
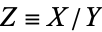has a Cauchy distribution with statistical median 
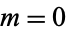and full width
 |
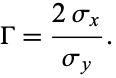(15)
|
The sum of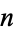 
variates each from a Cauchy distribution has itself a Cauchy distribution, as can be seen from
where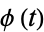 
is the characteristic function and ](https://mathworld.wolfram.com/images/equations/CauchyDistribution/Inline53.gif)
is the inverse Fourier transform, taken with parameters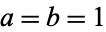 
.
REFERENCES:
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 104, 1984.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 114-115, 1992.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
