تسجيل الدخول

تسجيل

Run

المؤلف:  Bloom, D. M.

المصدر:  "Probabilities of Clumps in a Binary Sequence (and How to Evaluate Them Without Knowing a Lot)." Math. Mag. 69

الجزء والصفحة:  ...

31-3-2021

3992

Run

A run is a sequence of more than one consecutive identical outcomes, also known as a clump.

Let 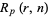 be the probability that a run of  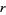or more consecutive heads appears in  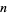independent tosses of a coin (i.e.,  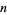Bernoulli trials). This is equivalent to repeated picking from an urn containing two distinguishable objects with replacement after each pick. Let the probability of obtaining a head be 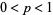. Then there is a beautiful formula for  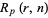given in terms of the coefficients of the generating function

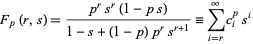(1)

(Feller 1968, p. 300). Then

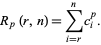(2)

The following table gives the triangle of numbers 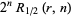 for 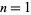, 2, ... and 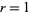, 2, ...,  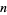(OEIS A050227).

Sloane	A000225	A008466	A050231	A050233
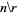	1	2	3	4	5	6	7	8
1	1	0	0	0	0	0	0	0
2	3	1	0	0	0	0	0	0
3	7	3	1	0	0	0	0	0
4	15	8	3	1	0	0	0	0
5	31	19	8	3	1	0	0	0
6	63	43	20	8	3	1	0	0
7	127	94	47	20	8	3	1	0
8	255	201	107	48	20	8	3	1

The special case 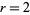 gives the sequence

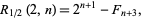(3)

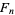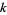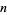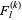where  is a Fibonacci number. Similarly, the probability that no  consecutive tails will occur in  tosses is given by , where  is a Fibonacci k-step number.

Feller (1968, pp. 278-279) proved that for ,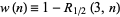

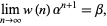(4)

where

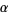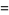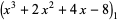			(5)
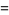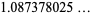			(6)

(OEIS A086253) is the positive root of the above polynomial and

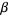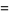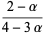			(7)
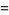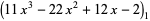			(8)
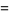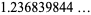			(9)

(OEIS A086254) is the positive root of the above polynomial. The corresponding constants for a run of 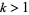 heads are 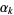, the smallest positive root of

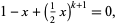(10)

and

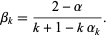(11)

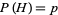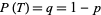These are modified for unfair coins with  and  to 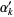, the smallest positive root of

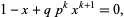(12)

and

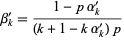(13)

(Feller 1968, pp. 322-325).

Given 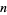 Bernoulli trials with a probability of success (heads) 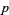, the expected number of tails is 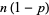, so the expected number of tail run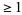s  is 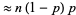. Continuing,

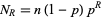(14)

is the expected number of runs 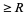. The longest expected run is therefore given by

(15)

(Gordon et al. 1986, Schilling 1990). Given 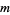 0s and  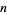1s, the number of possible arrangements with  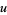runs is

{2(m-1; k-1)(n-1; k-1) u=2k; (m-1; k)(n-1; k-1)+(m-1; k-1)(n-1; k) u=2k+1 " src="https://mathworld.wolfram.com/images/equations/Run/NumberedEquation11.gif" style="height:78px; width:324px" />

(16)

for 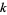 an integer, where  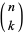is a binomial coefficient (Johnson and Kotz 1968, p. 268). Then

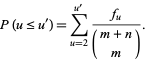(17)

Now instead consider picking of 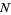 objects without replacement from a collection of  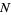containing  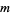indistinguishable objects of one type and  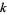indistinguishable objects of another. Let  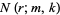denote the number of permutations of these objects in which no 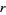-run occurs. For example, there are 6 permutations of two objects of type  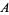and two of type 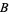. Of these, 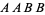, , 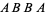, 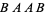and 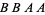 contain runs of length two, so 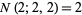. In general, the probability that an 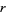-run does occur is given by

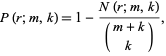(18)

where 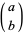 is a binomial coefficient. Bloom (1996) gives the following recurrence sequence for ,

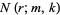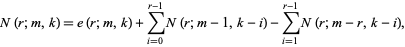(19)

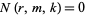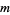where  for  or 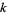 negative and

{1 if m=0 and 0<=k<r; -1 if m=r and 0<=k<r; 0 otherwise. " src="https://mathworld.wolfram.com/images/equations/Run/NumberedEquation15.gif" style="height:62px; width:238px" />

(20)

Another recurrence which has only a fixed number of terms is given by

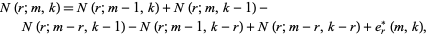(21)

where

{1 if (m,k)=(0,0) or (r,r); -1 if (m,k)=(0,r) or (r,0); 0 otherwise " src="https://mathworld.wolfram.com/images/equations/Run/NumberedEquation17.gif" style="height:62px; width:246px" />

(22)

(Goulden and Jackson 1983, Bloom 1996).

These formulas can be used to calculate the probability of obtaining a run of 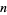 cards of the same color in a deck of 52 cards. For 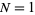, 2, ..., this yields the sequence 1, 247959266474051/247959266474052, ... (OEIS A086439 and A086440). Normalizing by multiplying by  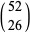gives 495918532948104, 495918532948102, 495891608417946, 483007233529142, ... (OEIS A086438). The result

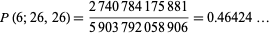(23)

disproves the assertion of Gardner (1982) that "there will almost always be a clump of six or seven cards of the same color" in a normal deck of cards.

Bloom (1996) gives the expected number of noncontiguous 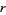-runs (i.e., split the sequence into maximal clumps of the same value and count the number of such clumps of length 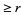) in a sequence of  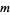0s and  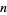1s as

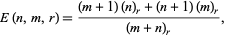(24)

where 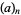 is the falling factorial. For 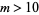,  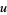has an approximately normal distribution with mean and variance

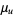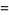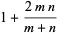			(25)
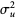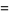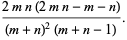			(26)

---

REFERENCES:

Bloom, D. M. "Probabilities of Clumps in a Binary Sequence (and How to Evaluate Them Without Knowing a Lot)." Math. Mag. 69, 366-372, 1996.

Feller, W. An Introduction to Probability Theory and Its Application, Vol. 1, 3rd ed. New York: Wiley, 1968.

Finch, S. R. "Feller's Coin Tossing Constants." §5.11 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 339-342, 2003.

Gardner, M. Aha! Gotcha: Paradoxes to Puzzle and Delight. New York: W. H. Freeman, p. 124, 1982.

Godbole, A. P. "On Hypergeometric and Related Distributions of Order 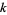." Commun. Stat.: Th. and Meth. 19, 1291-1301, 1990.

Godbole, A. P. and Papastavridis, G. (Eds.). Runs and Patterns in Probability: Selected Papers. New York: Kluwer, 1994.

Gordon, L.; Schilling, M. F.; and Waterman, M. S. "An Extreme Value Theory for Long Head Runs." Prob. Th. and Related Fields 72, 279-287, 1986.

Goulden, I. P. and Jackson, D. M. Combinatorial Enumeration. New York: Wiley, 1983.

Johnson, N. and Kotz, S. Discrete Distributions. New York: Wiley, 1968.

Mood, A. M. "The Distribution Theory of Runs." Ann. Math. Statistics 11, 367-392, 1940.

Philippou, A. N. and Makri, F. S. "Successes, Runs, and Longest Runs." Stat. Prob. Let. 4, 211-215, 1986.

Schilling, M. F. "The Longest Run of Heads." Coll. Math. J. 21, 196-207, 1990.

Schuster, E. F. In Runs and Patterns in Probability: Selected Papers (Ed. A. P. Godbole and S. Papastavridis). Boston, MA: Kluwer, pp. 91-111, 1994.

Sloane, N. J. A. Sequences A000225/M2655, A008466, A050227, A050231, A050232, A050233, A086253, A086254, A086438, A086439, and A086440 in "The On-Line Encyclopedia of Integer Sequences."