Mills Ratio
المؤلف:
Boyd, A. V.
المصدر:
"Inequalities for Mills, Ratio." Rep. Stat. Appl. Res. (Union Japan. Sci. Eng.) 6
الجزء والصفحة:
...
11-3-2021
2502
Mills Ratio
The Mills ratio is defined as
where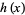 
is the hazard function, 
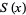is the survival function, 
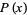is the probability density function, and 
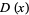is the distribution function.
For example, for the normal distribution,
![m_(normal)(x)=e^((x-mu)^2/(2sigma^2))sqrt(pi/2)[1erf((x-mu)/(sqrt(2)sigma))],](https://mathworld.wolfram.com/images/equations/MillsRatio/NumberedEquation1.gif) |
(4)
|
which simplifies to
![m_(standard normal)(x)=e^(x^2/2)sqrt(pi/2)erfc(x/(sqrt(2))]](https://mathworld.wolfram.com/images/equations/MillsRatio/NumberedEquation2.gif) |
(5)
|
for the standard normal distribution. The latter function has the particularly simple continued fraction representation
 |
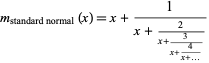(6)
|
(Cuyt et al. 2010, p. 376).
REFERENCES:
Boyd, A. V. "Inequalities for Mills' Ratio." Rep. Stat. Appl. Res. (Union Japan. Sci. Eng.) 6, 44-46, 1959.
Cuyt, A.; Brevik Petersen, V.; Verdonk, B.; Waadeland, H.; and Jones, W. B. Handbook of Continued Fractions for Special Functions. New York: Springer, 2010.
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, p. 13, 2000.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
