Let two players each have a finite number of pennies (say, 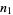 for player one and  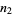for player two). Now, flip one of the pennies (from either player), with each player having 50% probability of winning, and transfer a penny from the loser to the winner. Now repeat the process until one player has all the pennies.

If the process is repeated indefinitely, the probability that one of the two player will eventually lose all his pennies must be 100%. In fact, the chances 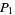 and 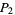 that players one and two, respectively, will be rendered penniless are

			(1)
			(2)

i.e., your chances of going bankrupt are equal to the ratio of pennies your opponent starts out to the total number of pennies.

Therefore, the player starting out with the smallest number of pennies has the greatest chance of going bankrupt. Even with equal odds, the longer you gamble, the greater the chance that the player starting out with the most pennies wins. Since casinos have more pennies than their individual patrons, this principle allows casinos to always come out ahead in the long run. And the common practice of playing games with odds skewed in favor of the house makes this outcome just that much quicker.

REFERENCES:

Cover, T. M. "Gambler's Ruin: A Random Walk on the Simplex." §5.4 in Open Problems in Communications and Computation. (Ed. T. M. Cover and B. Gopinath). New York: Springer-Verlag, p. 155, 1987.

Hajek, B. "Gambler's Ruin: A Random Walk on the Simplex." §6.3 in Open Problems in Communications and Computation. (Ed. T. M. Cover and B. Gopinath). New York: Springer-Verlag, pp. 204-207, 1987.

Kraitchik, M. "The Gambler's Ruin." §6.20 in Mathematical Recreations. New York: W. W. Norton, p. 140, 1942.