The 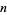th raw moment  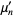(i.e., moment about zero) of a distribution  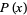is defined by

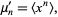(1)

where

{sumf(x)P(x) discrete distribution; intf(x)P(x)dx continuous distribution. " src="https://mathworld.wolfram.com/images/equations/Moment/NumberedEquation2.gif" style="height:68px; width:306px" />

(2)

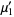, the mean, is usually simply denoted 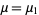. If the moment is instead taken about a point ,

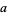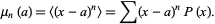(3)

A statistical distribution is not uniquely specified by its moments, although it is by its characteristic function.

The moments are most commonly taken about the mean. These so-called central moments are denoted 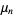 and are defined by

			(4)
			(5)

with 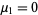. The second moment about the mean is equal to the variance

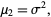(6)

where 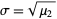 is called the standard deviation.

The related characteristic function is defined by

			(7)
			(8)

The moments may be simply computed using the moment-generating function,

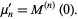(9)

REFERENCES:

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 145-149, 1984.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Moments of a Distribution: Mean, Variance, Skewness, and So Forth." §14.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 604-609, 1992.