تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Poulet Number
المؤلف:
Guy, R. K.
المصدر:
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag
الجزء والصفحة:
...
25-1-2021
1089
+
-
20
Poulet Number
A Poulet number is a Fermat pseudoprime to base 2, denoted psp(2), i.e., a composite number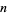 
such that
 |
The first few Poulet numbers are 341, 561, 645, 1105, 1387, ... (OEIS A001567).
Pomerance et al. (1980) computed all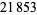 
Poulet numbers less than 
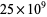. The numbers less than 
, 
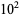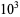, ..., are 0, 3, 22, 78, 245, ... (OEIS A055550).
Pomerance has shown that the number of Poulet numbers less than 
for sufficiently large 
satisfy
![exp[(lnx)^(5/14)]<P_2(x)<xexp(-(lnxlnlnlnx)/(2lnlnx))](https://mathworld.wolfram.com/images/equations/PouletNumber/NumberedEquation2.gif) |
(Guy 1994).
A Poulet number all of whose divisors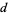 
satisfy 
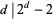is called a super-Poulet number. There are an infinite number of Poulet numbers which are not super-Poulet numbers. Shanks (1993) calls any integer satisfying 
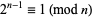(i.e., not limited to odd composite numbers) a Fermatian.
REFERENCES:
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 28-29, 1994.
Pinch, R. G. E. "The Pseudoprimes Up to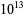 
." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
Pomerance, C.; Selfridge, J. L.; and Wagstaff, S. S. Jr. "The Pseudoprimes to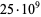 
." Math. Comput. 35, 1003-1026, 1980. http://mpqs.free.fr/ThePseudoprimesTo25e9.pdf.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 115-117, 1993.
Sloane, N. J. A. Sequences A001567/M5441 and A055550 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
