Euclid's second theorem states that the number of primes is infinite. The proof of this can be accomplished using the numbers

			(1)
			(2)

known as Euclid numbers, where 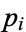 is the 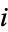th prime and  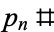is the primorial.

The first few Euclid numbers are 3, 7, 31, 211, 2311, 30031, 510511, 9699691, 223092871, 6469693231, ... (OEIS A006862; Tietze 1965, p. 19).

The indices 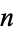 of the first few prime Euclid numbers  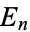are 1, 2, 3, 4, 5, 11, 75, 171, 172, 384, 457, 616, 643, ... (OEIS A014545), so the first few Euclid primes (commonly known as primorial primes) are 3, 7, 31, 211, 2311, 200560490131, ... (OEIS A018239). The largest known Euclid number is 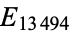, and it is not known if there are an infinite number of prime Euclid numbers (Guy 1994, Ribenboim 1996).

The largest factors of 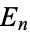 for 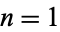, 2, ... are 3, 7, 31, 211, 2311, 509, 277, 27953, ... (OEIS A002585).

REFERENCES:

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.

Guy, R. and Nowakowski, R. "Discovering Primes with Euclid." Delta (Waukesha) 5, 49-63, 1975.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 28, 2003.

Naur, T. "Mullin's Sequence of Primes Is Not Monotonic." Proc. Amer. Math. Soc. 90, 43-44, 1984.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.

Sloane, N. J. A. Sequences A006862/M2698, A002585/M2697, A014545, and A018239 in "The On-Line Encyclopedia of Integer Sequences."

Tietze, H. Famous Problems of Mathematics: Solved and Unsolved Mathematics Problems from Antiquity to Modern Times. New York: Graylock Press, 1965.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 35-37, 1991.

Wagstaff, S. S., Jr. "Computing Euclid's Primes." Bull. Inst. Combin. Appl. 8, 23-32, 1993.