
Bernoulli Triangle
 المؤلف:
MacWilliams, F. J. and Sloane, N. J. A.
المؤلف:
MacWilliams, F. J. and Sloane, N. J. A.
 المصدر:
The Theory of Error-Correcting Codes. Amsterdam, Netherlands: North-Holland
المصدر:
The Theory of Error-Correcting Codes. Amsterdam, Netherlands: North-Holland
 الجزء والصفحة:
...
الجزء والصفحة:
...
 6-1-2021
6-1-2021
 1610
1610
Bernoulli Triangle
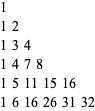 |
(1)
|
The number triangle illustrated above (OEIS A008949) composed of the partial sums of binomial coefficients,
where 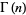 is a gamma function and
is a gamma function and 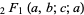 is a hypergeometric function.
is a hypergeometric function.

The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Bernoulli triangle.
REFERENCES:
Kirillov, A. A. "Variations on the Triangular Theme." In Lie Groups and Lie Algebras: E. B. Dynkin's Seminar: Dedicated to E. B. Dynkin on the Occasion of His Seventieth Birthday (Ed. S. G. Gindikin and E. B. Vinberg.) Providence, RI: Amer. Math. Soc., pp. 43-73, 1995.
MacWilliams, F. J. and Sloane, N. J. A. The Theory of Error-Correcting Codes. Amsterdam, Netherlands: North-Holland, p. 376, 1978.
Sloane, N. J. A. Sequence A008949 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


