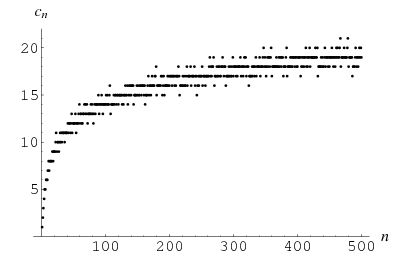
The complexity 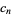 of an integer  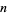is the least number of 1s needed to represent it using only additions, multiplications, and parentheses. For example, the numbers 1 through 10 can be minimally represented as

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)
			(7)
			(8)
			(9)
			(10)
			(11)
			(12)
			(13)

so the complexities for 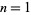, 2, ..., are 1, 2, 3, 4, 5, 5, 6, 6, 6, 7, 8, 7, 8, ... (OEIS A005245).

The smallest numbers of complexity 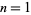, 2, ... are 1, 2, 3, 4, 5, 7, 10, 11, 17, 22, 23, 41, ... (OEIS A005520).

REFERENCES:

Guy, R. K. "Expressing Numbers Using Just Ones." §F26 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 263, 1994.

Guy, R. K. "Some Suspiciously Simple Sequences." Amer. Math. Monthly 93, 186-190, 1986.

Guy, R. K. "Monthly Unsolved Problems, 1969-1987." Amer. Math. Monthly 94, 961-970, 1987.

Guy, R. K. "Unsolved Problems Come of Age." Amer. Math. Monthly 96, 903-909, 1989.

Pegg, E. Jr. "Math Games: Integer Complexity." Feb. 12, 2004. https://www.maa.org/editorial/mathgames/mathgames_04_12_04.html.

Pegg, E. Jr. "Integer Complexity." https://library.wolfram.com/infocenter/MathSource/5175/.

Rawsthorne, D. A. "How Many 1's are Needed?" Fib. Quart. 27, 14-17, 1989.

Sloane, N. J. A. Sequences A005245/M0457 and A005520/M0523 in "The On-Line Encyclopedia of Integer Sequences."

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 916, 2002.