Lagrange,s Four-Square Theorem
المؤلف:
Hardy, G. H.
المصدر:
Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
الجزء والصفحة:
...
27-12-2020
1346
Lagrange's Four-Square Theorem
A theorem, also known as Bachet's conjecture, which Bachet inferred from a lack of a necessary condition being stated by Diophantus. It states that every positive integer can be written as the sum of at most four squares. Although the theorem was proved by Fermat using infinite descent, the proof was suppressed. Euler was unable to prove the theorem. The first published proof was given by Lagrange in 1770 and made use of the Euler four-square identity.
Lagrange proved that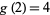 
, where 4 may be reduced to 3 except for numbers of the form 
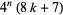, as proved by Legendre in 1798 (Nagell 1951, p. 194; Wells 1986, pp. 48 and 56; Hardy 1999, p. 12; Savin 2000).
REFERENCES:
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "The Four-Square Theorem." §20.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 302-303, 1979.
Landau, E. Vorlesungen über Zahlentheorie, Vol. 1. New York: Chelsea, pp. 114-122, 1970.
Nagell, T. "Bachet's Theorem." §55 in Introduction to Number Theory. New York: Wiley, pp. 191-195, 1951.
Niven, I. M.; Zuckerman, H. S.; and Montgomery, H. L. An Introduction to the Theory of Numbers, 5th ed. New York: Wiley, 1991.
Savin, A. "Shape Numbers." Quantum 11, 14-18, 2000.
Séroul, R. "Sums of Four Squares." §8.13 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 207-208, 2000.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 48, 1986.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
