تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Star Number
المؤلف:
Conway, J. H. and Guy, R. K
المصدر:
The Book of Numbers. New York: Springer-Verlag
الجزء والصفحة:
...
22-12-2020
1201
+
-
20
Star Number
The number of cells in a generalized Chinese checkers board (or "centered" hexagram). Unlike the polygonal numbers, there is ambiguity in the case of the star numbers as to whethe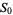r 
or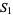 
should be set equal to 1, since the equation defining star numbers never gives 0. For consistency with other figurate numbers, which are all defined such that 
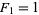, that definition is used here as well, and 
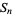is defined by
 |
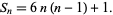(1) |
The first few for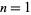 
, 2, ... are 1, 13, 37, 73, 121, ... (OEIS A003154), and the generating function for the star numbers is
 |
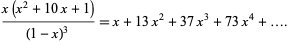(2) |
The star numbers satisfy the linear recurrence equation
 |
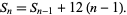(3) |
Every star number has digital root 1 or 4, and the final digit must be one of 1, 3, or 7, and the final two digits must be one of 01, 13, 21, 33, 37, 41, 53, 61, 73, 81, or 93.
The first few triangular star numbers are 1, 253, 49141, 9533161, ... (OEIS A006060), and can be computed using
 |
 |
![(3[(7+4sqrt(3))^(2n-1)+(7-4sqrt(3))^(2n-1)]-10)/(32)](https://mathworld.wolfram.com/images/equations/StarNumber/Inline8.gif) |
(4) |
 |
 |
 |
(5) |
The indices of the corresponding triangular numbers are 1, 22, 313, 4366, 60817, ... (OEIS A068774), and of the star numbers are 1, 7, 91, 1261, 17557, ... (OEIS A068775).
The first few square star numbers are 1, 121, 11881, 1164241, 114083761, ... (OEIS A006061). The indices of the corresponding square numbers are 1, 11, 109, 1079, 10681, 105731, 1046629, ... (OEIS A054320), and of the star numbers are 1, 5, 45, 441, 4361, 43165, 427285, ... (OEIS A068778). Square star numbers are obtained by solving the Diophantine equation
 |
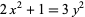(6) |
and can be computed using
![SS_n=([(5+2sqrt(6))^n(sqrt(6)-2)-(5-2sqrt(6))^n(sqrt(6)+2)]^2)/4.](https://mathworld.wolfram.com/images/equations/StarNumber/NumberedEquation5.gif) |
(7) |
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 41, 1996.
Gardner, M. "Hexes and Stars." Ch. 2 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 15-24, 1988.
Hindin, H. "Stars, Hexes, Triangular Numbers, and Pythagorean Triples." J. Recr. Math. 16, 191-193, 1983-1984.
Sloane, N. J. A. Sequences A003154/M4893, A006060/M5425, A006061/M5385, A054320, A068774, A068775, and A068778 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
