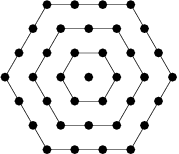
A hex number, also called a centered hexagonal number, is given by

			(1)
			(2)

where 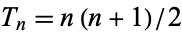 is the 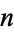th triangular number and the indexing with  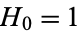is used following Conway and Guy (1996). The first few hex numbers for 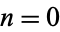, 1, ... are 1, 7, 19, 37, 61, 91, 127, 169, ... (OEIS A003215).

The hex numbers satisfy the recurrence equation

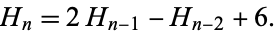(3)

The generating function of the hex numbers is

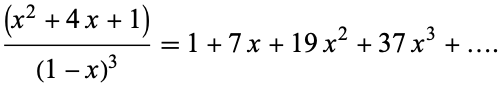(4)

The hex numbers are related to the cubic numbers by

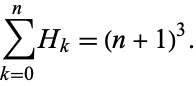(5)

This follows immediately from the fact that 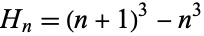, giving a telescoping sum.

The first triangular hex numbers are 1, 91, 8911, 873181, 85562821, ... (OEIS A006244). These correspond to indices 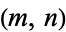 of triangular and hex numbers  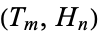of 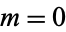, 5, 54, 539, 5340, 52865, 523314, 5180279, 51279480, ... (OEIS A087125) and 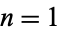, 13, 133, 1321, 13081, 129493, 1281853, ... (OEIS A031138). These are given by solving the Diophantine equation

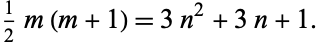(6)

The first few square hex numbers are 1, 169, 32761, 6355441, ... (OEIS A006051). These correspond to indices 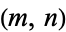 of triangular and hex numbers  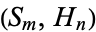of 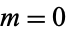, 7, 104, 1455, 20272, 282359, 3932760, ... (OEIS A001921) and 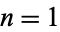, 13, 181, 2521, 35113, 489061, 6811741, ... (OEIS A001570). These are given by solving the Diophantine equation

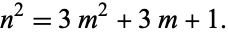(7)

The only hex number that is both square and triangular is 1.

There are no cubic hex numbers.

The prime hex numbers are sometimes known as Cuban primes.

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 41, 1996.

Gardner, M. "Hexes and Stars." Ch. 2 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 15-25, 1988.

Hindin, H. "Stars, Hexes, Triangular Numbers, and Pythagorean Triples." J. Recr. Math. 16, 191-193, 1983-1984.

Sloane, N. J. A. Sequences A001570/M4915, A001921/M4455, A003215/M4362, A006051/M5409, A006244/M5363, A031138 and A087125 in "The On-Line Encyclopedia of Integer Sequences."