Write down the positive integers in row one, cross out every 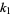th number, and write the partial sums of the remaining numbers in the row below. Now cross off every 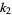th number and write the partial sums of the remaining numbers in the row below. Continue. For every positive integer 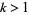, if every 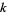th number is ignored in row 1, every 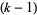th number in row 2, and every 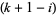th number in row 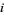, then the 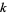th row of partial sums will be the 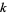th powers , , , ....

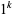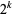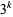REFERENCES:

Conway, J. H. and Guy, R. K. "Moessner's Magic." In The Book of Numbers. New York: Springer-Verlag, pp. 63-65, 1996.

Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 268-277, 1991.

Long, C. T. "On the Moessner Theorem on Integral Powers." Amer. Math. Monthly 73, 846-851, 1966.

Long, C. T. "Strike it Out--Add it Up." Math. Mag. 66, 273-277, 1982.

Moessner, A. "Eine Bemerkung über die Potenzen der natürlichen Zahlen." S.-B. Math.-Nat. Kl. Bayer. Akad. Wiss. 29, 1952.

Paasche, I. "Ein neuer Beweis des moessnerischen Satzes." S.-B. Math.-Nat. Kl. Bayer. Akad. Wiss. 1952, 1-5, 1953.

Paasche, I. "Ein zahlentheoretische-logarithmischer 'Rechenstab.' " Math. Naturwiss. Unterr. 6, 26-28, 1953-54.

Paasche, I. "Eine Verallgemeinerung des moessnerschen Satzes." Compositio Math. 12, 263-270, 1956.