Figurate Number
المؤلف:
Conway, J. H. and Guy, R. K.
المصدر:
The Book of Numbers. New York: Springer-Verlag
الجزء والصفحة:
...
12-12-2020
2686
Figurate Number
A figurate number, also (but mostly in texts from the 1500 and 1600s) known as a figural number (Simpson and Weiner 1992, p. 587), is a number that can be represented by a regular geometrical arrangement of equally spaced points. If the arrangement forms a regular polygon, the number is called a polygonal number. The polygonal numbers illustrated above are called triangular, square, pentagonal, and hexagonal numbers, respectively. Figurate numbers can also form other shapes such as centered polygons, L-shapes, three-dimensional solids, etc.
The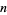 
th regular 
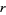-polytopic number is given by
where 
is the multichoose function,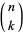 
is a binomial coefficient, and 
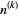is a rising factorial. Special cases therefore include the triangular numbers
 |
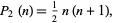(4)
|
tetrahedral numbers
 |
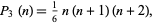(5)
|
pentatope numbers
 |
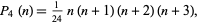(6)
|
and so on (Dickson 2005, p. 7).
The following table lists the most common types of figurate numbers.
| figurate number |
formula |
| biquadratic number |
 |
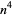| centered cube number |
 |
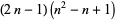| centered pentagonal number |
 |
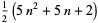| centered square number |
 |
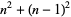| centered triangular number |
 |
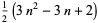| cubic number |
 |
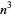| decagonal number |
 |
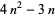| gnomonic number |
 |
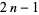| Haűy octahedral number |
 |
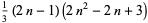| Haűy rhombic dodecahedral number |
 |
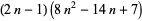| heptagonal number |
 |
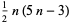| hex number |
 |
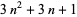| heptagonal pyramidal number |
 |
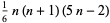| hexagonal number |
 |
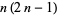| hexagonal pyramidal number |
 |
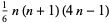| octagonal number |
 |
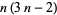| octahedral number |
 |
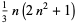| pentagonal number |
 |
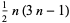| pentagonal pyramidal number |
 |
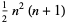| pentatope number |
 |
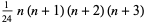| pronic number |
 |
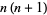| rhombic dodecahedral number |
 |
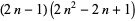| square number |
 |
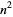| square pyramidal number |
 |
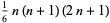| stella octangula number |
 |
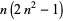| tetrahedral number |
 |
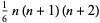| triangular number |
 |
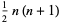| truncated octahedral number |
 |
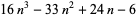| truncated tetrahedral number |
 |
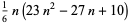REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 30-62, 1996.
Dickson, L. E. "Polygonal, Pyramidal, and Figurate Numbers." Ch. 1 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Chelsea, pp. 1-39, 2005.
Goodwin, P. "A Polyhedral Sequence of Two." Math. Gaz. 69, 191-197, 1985.
Guy, R. K. "Figurate Numbers." §D3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 147-150, 1994.
Kraitchik, M. "Figurate Numbers." §3.4 in Mathematical Recreations. New York: W. W. Norton, pp. 66-69, 1942.
Savin, A. "Shape Numbers." Quantum 11, 14-18, 2000.
Simpson, J. A. and Weiner, E. S. C. (Preparers). The Compact Oxford English Dictionary, 2nd ed. Oxford, England: Clarendon Press, 1992.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
