A number 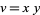 with an even number  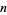of digits formed by multiplying a pair of 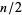-digit numbers (where the digits are taken from the original number in any order)  and 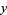 together. Pairs of trailing zeros are not allowed. If  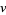is a vampire number, then  and 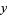 are called its "fangs." Examples of vampire numbers include

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)
			(7)

(OEIS A014575). The 8-digit vampire numbers are 10025010, 10042510, 10052010, 10052064, 10081260, ... (OEIS A048938) and the 10-digit vampire numbers are 1000174288, 1000191991, 1000198206, 1000250010, ... (OEIS A048939). The numbers of 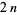-digit vampires are 0, 7, 148, 3228, ... (OEIS A048935).

Vampire numbers having two distinct pairs of fangs include

			(8)
			(9)
			(10)

(OEIS A048936).

Vampire numbers having three distinct pairs of fangs include

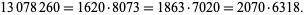(11)

(OEIS A048937).

The first vampire numbers with four pairs of fangs are

			(12)
			(13)
			(14)
			(15)

and

			(16)
			(17)
			(18)
			(19)

and the first vampire number with five pairs of fangs is

			(20)
			(21)
			(22)
			(23)
			(24)

(J. K. Andersen, pers. comm., May 4, 2003).

General formulas can be constructed for special classes of vampires, such as the fangs

			(25)
			(26)

giving the vampire

			(27)
			(28)
			(29)
			(30)

where 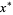 denotes  with the digits reversed (Roush and Rogers 1997-1998).

Pickover (1995) also defines pseudovampire numbers, in which the multiplicands have different numbers of digits.

REFERENCES:

Anderson, J. K. "Vampire Numbers." https://hjem.get2net.dk/jka/math/vampires/.

Childs, J. "Vampire Numbers!" https://www.grenvillecc.ca/faculty/jchilds/vampire.htm.

Childs, J. "Vampire Numbers! Part 2." https://www.grenvillecc.ca/faculty/jchilds/vampire2.htm.

Childs, J. "Vampire Numbers--Information Summary--Part 3." https://www.grenvillecc.ca/faculty/jchilds/vampire3.htm.

Pickover, C. A. "Vampire Numbers." Ch. 30 in Keys to Infinity. New York: Wiley, pp. 227-231, 1995.

Pickover, C. A. "Vampire Numbers." Theta 9, 11-13, Spring 1995.

Pickover, C. A. "Interview with a Number." Discover 16, 136, June 1995.

Rivera, C. "Problems & Puzzles: Puzzle 199-The Prime-Vampire Numbers." https://www.primepuzzles.net/puzzles/puzz_199.htm.

Roush, F.W.; Rogers, D. G. "Tame Vampires." Math. Spectrum 30, 37-39, 1997-1998.