Tangent Number
المؤلف:
Borwein, J. and Bailey, D.
المصدر:
Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
الجزء والصفحة:
...
7-11-2020
1387
Tangent Number
The tangent numbers, also called a zag number, and given by
 |
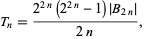(1)
|
where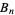 
is a Bernoulli number, are numbers that can be defined either in terms of a generating function given as the Maclaurin series of 
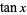or as the numbers of alternating permutations on 
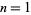, 3, 5, 7, ... symbols (where permutations that are the reverses of one another counted as equivalent). The first few 
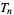for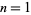 
, 2, ... are 1, 2, 16, 272, 7936, ... (OEIS A000182).
For example, the reversal-nonequivalent alternating permutations on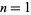 
and 3 numbers are ![<span style=]()
{1}" src="https://mathworld.wolfram.com/images/equations/TangentNumber/Inline7.gif" style="height:15px; width:17px" />, and ![<span style=]()
{1,3,2}" src="https://mathworld.wolfram.com/images/equations/TangentNumber/Inline8.gif" style="height:15px; width:47px" />, ![<span style=]()
{2,1,3}" src="https://mathworld.wolfram.com/images/equations/TangentNumber/Inline9.gif" style="height:15px; width:47px" />, respectively.
The tangent numbers have the generating function
Shanks (1967) defines a generalization of the tangent numbers by
 |
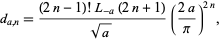(5)
|
where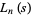 
is a Dirichlet L-series, giving the special case
 |
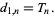(6)
|
The following table gives the first few values of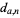 
for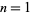 
, 2, ....
 |
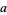OEIS |
 |
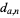| 1 |
A000182 |
1, 2, 16, 272, 7936, ... |
| 2 |
A000464 |
1, 11, 361, 24611, ... |
| 3 |
A000191 |
2, 46, 3362, 515086, ... |
| 4 |
A000318 |
4, 128, 16384, 4456448, ... |
| 5 |
A000320 |
4, 272, 55744, 23750912, ... |
| 6 |
A000411 |
6, 522, 152166, 93241002, ... |
| 7 |
A064072 |
8, 904, 355688, 296327464, ... |
| 8 |
A064073 |
8, 1408, 739328, 806453248, ... |
| 9 |
A064074 |
12, 2160, 1415232, 1951153920, ... |
| 10 |
A064075 |
14, 3154, 2529614, 4300685074, ... |
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Knuth, D. E. and Buckholtz, T. J. "Computation of Tangent, Euler, and Bernoulli Numbers." Math. Comput. 21, 663-688, 1967.
Shanks, D. "Generalized Euler and Class Numbers." Math. Comput. 21, 689-694, 1967.
Shanks, D. Corrigendum to "Generalized Euler and Class Numbers." Math. Comput. 22, 699, 1968.
Sloane, N. J. A. Sequence A000182/M2096 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
