التقريب الكظيم Adiabatic Approximation

يمكن جمع عناصر المصفوفة في حدود قطرية C_mm وحدود قطرية C_mm(n≠m) الحدود القطرية تساوي:

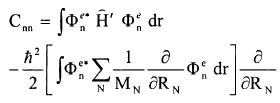.......................(1)

بتبادل التفاضل بالنسبة الى الاحداثيات النووية والتكامل على الاحداثيات الالكترونية في الحد الثاني من المعادلة 1 فان النتيجة ستكون صفرا، لان 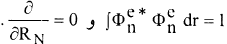 وباستخدام المعادلة:

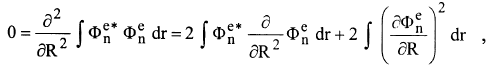
فان الحد الاول يمكن كتابته كالآتي:

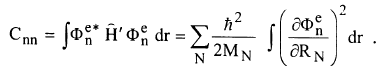...........................(2)

الحدود القطرية تعتمد تربيعيا على التغير في الدالة الموجية Φ^e_n عند تغير الاحداثيات النووية. هذه الحدود صغيرة القيمة لان الكتل النووية M_N في المقام قيمتها كبيرة. عند تعويض المعادلة 2 في المعادلة (i) 

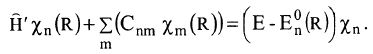.............(i)

نحصل على التقريب الكظيم:

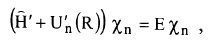............................(3)

وبالجهد (U^'_n(R يعطى بالمعادلة:

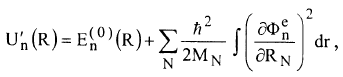
وهو يختلف عن الجهد في تقريب بورن – اوبنهايمر (E⁽⁰⁾_n(R بالحد التصحيحي الذي يعتمد على الكتلة النووية ولذلك تختلف قيمته باختلاف نظائر العنصر الكيميائي.

يمكن النظر الى التقريب الكظيم كما ياتي: ان السحابة الالكترونية لا تتبع التغير في الحركة النووية آنيا ولكن توجد فترة تاخير زمنية تعتمد على مقدار الطاقة النووية ولا تمزج الحركة النووية بين حالتين الكترونيتين والتقريب الكظيم يعتبر خطوة اضافية بالنسبة الى تقريب بورن – اوبنهايمر وتصحيحه ضئيل المقدار لان الكتل النووية كبيرة.

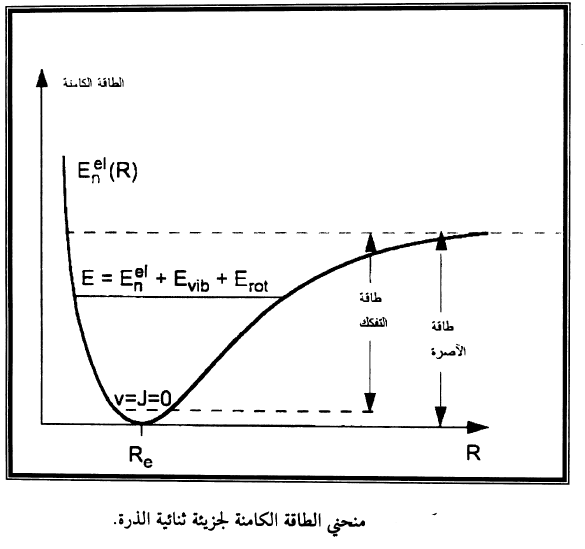
توصف الطاقة الالكترونية (E⁽⁰⁾_n(R في التقريب الكظيم كسطح طاقة كامنة في فضاء الاحداثيات النووية {R= {R₁,R₂,....R_n وتمثل الجهد الذي تتحرك النواة فيه وللجزيئات الثنائية الذرة يختزل هذا الجهد الى متغير واحد |R=|R₁-R₂ وهو المسافة بين النواتين. منحني الطاقة الكامنة (E⁽⁰⁾_n(R)=V(R  مبين في شكل 1 لجزيئة ثنائية الذرة ويمر المنحني بقيمة صغرى عند المسافة R_e وتدعى مسافة الاتزان وعمق الجهد عند المسافة الصغرى يمثل طاقة الاصرة 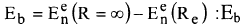 للحالة الالكترونية n.

الطاقة اللازمة لتفكيك الجزيئة في اوطأ مستوى اهتزازي v=0 تدعى طاقة التفكك E_d.

الطاقة الكلية للجزيئة في الحالة n تساوي مجموع الحدود الاتية:

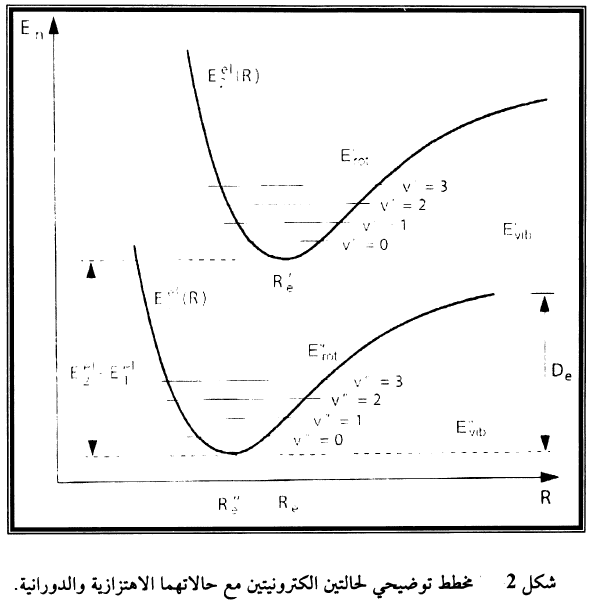
توجد لكل حالة الكترونية مجموعة من الحالات الاهتزازية متميزة بالعدد الاهتزازي الكمي v، ولكل حالة اهتزازية يوجد عادة عدد كبير جدا من الحالات الدورانية متميزة بالعدد الدوراني الكمي J كما مبين في شكل 2.

الشكل (1)

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشبابيك: تقديم أكثر من 50 ألف وجبة طعام لزائري الأربعين

قسم الشؤون الخدمية يطلق حملة تنظيف لمنطقة باب بغداد بعد انتهاء زيارة الأربعين

قسم الشؤون الفكرية: نحو 5000 مستفيد من خدمات محطة مجمّع سيد الماء الثقافي

مجمع أبي الفضل العباس (عليه السلام): أكثر من 30 ألف مستفيدة من الخدمات الصحية في زيارة الأربعين

المزيد

الآخبار الصحية

"ساعة الذئب" تؤرق الملايين.. حل علمي ينقذ نومك

يخفف الألم.. معجون أسنان مصنوع من الشعر ؟!

كوابيسك ليست عشوائية.. ماذا تحاول أن تخبرك؟

5 مخاطر غير متوقعة لتناول البروتين بكثرة

المزيد

الآخبار التكنلوجية

أندرويد 16 على الأبواب..هاتفك سيصبح وكيلك الذكي !

"غوغل" مهددة ببيع متصفحها الشهير "كروم".. من المشتري؟

"ناسا" و"غوغل" تطوران مساعدا طبيا ذكيا لمرافقة رواد الفضاء

هل تشغيل تكييف السيارة على "الحد الأقصى" ضار؟

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon