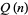, also denoted  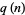(Abramowitz and Stegun 1972, p. 825), gives the number of ways of writing the integer  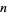as a sum of positive integers without regard to order with the constraint that all integers in a given partition are distinct. For example, 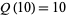, since the partitions of 10 into distinct parts are {1,2,3,4}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline5.gif" style="height:15px; width:62px" />, {2,3,5}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline6.gif" style="height:15px; width:47px" />, {1,4,5}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline7.gif" style="height:15px; width:47px" />, {1,3,6}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline8.gif" style="height:15px; width:47px" />, {4,6}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline9.gif" style="height:15px; width:32px" />, {1,2,7}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline10.gif" style="height:15px; width:47px" />, {3,7}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline11.gif" style="height:15px; width:32px" />, {2,8}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline12.gif" style="height:15px; width:32px" />, {1,9}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline13.gif" style="height:15px; width:32px" />, {10}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline14.gif" style="height:15px; width:24px" />. The 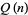 function is implemented in the Wolfram Language as PartitionsQ[n].  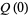is generally defined to be 1.

The values for 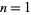, 2, ... are 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (OEIS A000009).

The first few prime values of 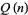 are for indices 3, 4, 5, 7, 22, 70, 100, 495, 1247, 2072, 320397, 3335367, 16168775, 37472505, 52940251, 78840125, 81191852, ... (OEIS A035359), corresponding to values 2, 2, 3, 5, 89, 29927, 444793, 602644050950309, ... (OEIS A051005), with no others up to  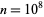(M. Alekseyev, Jul. 10, 2015).

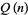 is also the number of partitions of  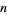with odd parts, sometimes denoted  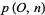(Andrews 1998, p. 237).

The generating function for 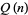 is

			(1)
			(2)
			(3)
			(4)
			(5)
			(6)

where 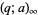 and 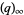 areq-Pochhammer symbols.

This can also be interpreted as another form of the Jacobi triple product, written in terms of the Q-functions as

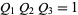(7)

(Borwein and Borwein 1987, p. 64).

A recurrence relation is given by 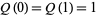 and

(8)

where

{sigma_1(n) for n an integer; 0 otherwise, " src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/NumberedEquation3.gif" style="height:41px; width:188px" />

(9)

and

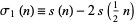(10)

is the odd divisor function giving the sum of odd divisors of 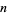: 1, 1, 4, 1, 6, 4, 8, ... (OEIS A000593; Abramowitz and Stegun 1972, p. 826).

Another recurrence relation is given by 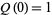 and

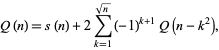(11)

where

{(-1)^j for n=j(3j+/-1)/2; 0 otherwise " src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/NumberedEquation6.gif" style="height:42px; width:213px" />

(12)

(E. Georgiadis, A. V. Sutherland, and K. S. Kedlaya; Sloane).

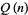 satisfies the inequality

(13)

for 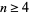.  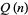has the asymptotic series

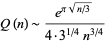(14)

(Abramowitz and Stegun 1972, p. 826).

A Rademacher-like convergent series for 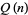 is given by

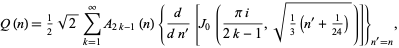(15)

where

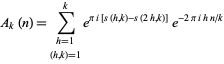(16)

(P. J. Grabner, pers. comm., Sep. 10, 2003; Hagis 1964ab, 1965), where 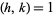 means 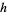 and 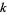 are relatively prime,

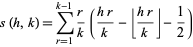(17)

is a Dedekind sum, 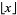 is the floor function, and  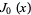is the zeroth order Bessel function of the first kind. Equation (16) corrects Abramowitz and Stegun (1972, p. 825), which erroneously state to be identical to the analogous expression in the formula for 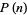). (15) can also be written explicitly as

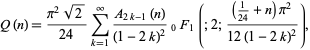(18)

where 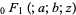 is a generalized hypergeometric function.

Let 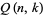 denote the number of ways of partitioning  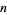into exactly  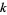distinct parts. For example,  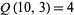since there are four partitions of 10 into three distinct parts: {1,2,7}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline62.gif" style="height:15px; width:47px" />, {1,3,6}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline63.gif" style="height:15px; width:47px" />, {1,4,5}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline64.gif" style="height:15px; width:47px" />, and {2,3,5}" src="https://mathworld.wolfram.com/images/equations/PartitionFunctionQ/Inline65.gif" style="height:15px; width:47px" />. 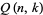 is given by

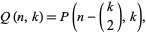(19)

where 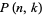 is the partition function P and  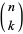is a binomial coefficient (Comtet 1974, p. 116). The following table gives the first few values of  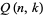(OEIS A008289; Comtet 1974, pp. 115-116).

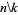	1	2	3	4
1	1
2	1
3	1	1
4	1	1
5	1	2
6	1	2	1
7	1	3	1
8	1	3	2
9	1	4	3
10	1	4	4	1

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Partitions into Distinct Parts." §24.2.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 825-826, 1972.

Andrews, G. E. The Theory of Partitions. Cambridge, England: Cambridge University Press, pp. 7-8, 1998.

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.

Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, pp. 114-115, 1974.

Hagis, P. Jr. "Partitions Into Odd and Unequal Parts." Amer. J. Math. 86, 317-324, 1964a.

Hagis, P. Jr. "On a Class of Partitions with Distinct Summands." Trans. Amer. Math. Soc. 112, 401-415, 1964b.

Hagis, P. Jr. "A Correction of Some Theorems on Partitions." Trans. Amer. Math. Soc. 118, 550, 1965.

Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 58, 1990.

Sloane, N. J. A. Sequences A000009/M0281, A000593/M3197, A008289, A035359 in "The On-Line Encyclopedia of Integer Sequences."