

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Prime Factor
المؤلف:
Conway, J. H.; Dietrich, H.; O,Brien, E. A.
المصدر:
"Counting Groups: Gnus, Moas, and Other Exotica." Math. Intell. 30
الجزء والصفحة:
...
15-9-2020
2325
Prime Factor
A prime factor is a factor that is prime, i.e., one that cannot itself be factored. In general, a prime factorization takes the form
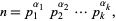 |
(1) |
where 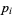 are prime factors and
are prime factors and 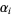 are their orders. Prime factorization can be performed in the Wolfram Language using the command FactorInteger[n], which returns a list of
are their orders. Prime factorization can be performed in the Wolfram Language using the command FactorInteger[n], which returns a list of 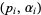 pairs.
pairs.
The following table gives the prime factorization for the positive integers 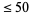 .
.
| 1 | 1 | 11 | 11 | 21 | 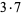 |
31 | 31 | 41 | 41 |
| 2 | 2 | 12 | 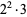 |
22 | 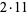 |
32 | 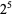 |
42 | 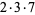 |
| 3 | 3 | 13 | 13 | 23 | 23 | 33 | 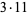 |
43 | 43 |
| 4 | 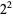 |
14 | 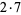 |
24 | 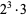 |
34 | 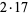 |
44 | 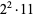 |
| 5 | 5 | 15 | 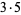 |
25 | 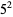 |
35 | 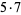 |
45 | 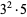 |
| 6 | 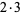 |
16 | 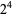 |
26 |  |
36 | 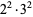 |
46 | 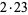 |
| 7 | 7 | 17 | 17 | 27 | 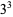 |
37 | 37 | 47 | 47 |
| 8 | 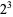 |
18 | 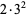 |
28 | 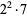 |
38 | 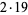 |
48 | 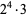 |
| 9 | 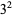 |
19 | 19 | 29 | 29 | 39 | 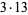 |
49 | 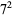 |
| 10 | 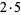 |
20 | 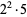 |
30 | 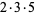 |
40 | 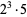 |
50 | 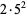 |
The number of not necessarily distinct prime factors of a number 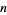 is denoted
is denoted 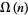 (Hardy and Wright 1979, p. 354) or
(Hardy and Wright 1979, p. 354) or 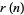 . Conway et al. (2008) coined the term "multiprimality of
. Conway et al. (2008) coined the term "multiprimality of 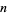 " to describe
" to describe 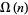 , with semiprimes then being termed biprimes, numbers with three factors terms triprimes, etc. The number of prime factors is given in terms of the prime factorization above by
, with semiprimes then being termed biprimes, numbers with three factors terms triprimes, etc. The number of prime factors is given in terms of the prime factorization above by
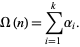 |
(2) |
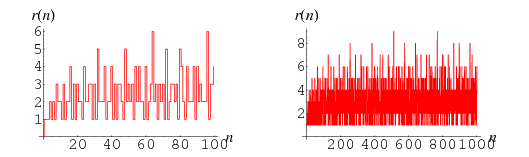
The first few values for 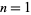 , 2, ... are 0, 1, 1, 2, 1, 2, 1, 3, 2, 2, 1, 3, 1, 2, 2, 4, 1, 3, 1, 3, ... (OEIS A001222).
, 2, ... are 0, 1, 1, 2, 1, 2, 1, 3, 2, 2, 1, 3, 1, 2, 2, 4, 1, 3, 1, 3, ... (OEIS A001222). 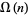 is plotted above up to
is plotted above up to 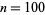 (left) and
(left) and 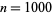 (right). The function
(right). The function 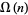 is implemented in the Wolfram Language as PrimeOmega[n],
is implemented in the Wolfram Language as PrimeOmega[n],
The function defined by 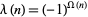 is known as the Liouville function.
is known as the Liouville function.
The number of distinct prime factors of a number 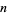 is denoted
is denoted 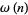 (Hardy and Wright 1979, p. 354), or sometimes
(Hardy and Wright 1979, p. 354), or sometimes 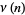 or
or 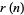 , and is implemented in the Wolfram Language as PrimeNu[n].
, and is implemented in the Wolfram Language as PrimeNu[n].
For example, 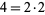 has a single distinct prime factor, so
has a single distinct prime factor, so 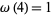 , but two total prime factors, so
, but two total prime factors, so 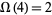 .
.
An asymptotic series for 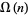 is given by
is given by
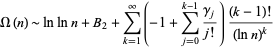 |
(3) |
(Diaconis 1976, Knuth 2000, Diaconis 2002, Finch 2003, Knuth 2003), where 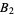 is a constant related to the Mertens constant and
is a constant related to the Mertens constant and 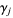 are Stieltjes constants. Furthermore, the variance is given by
are Stieltjes constants. Furthermore, the variance is given by
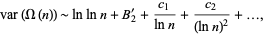 |
(4) |
where
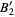 |
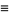 |
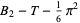 |
(5) |
 |
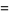 |
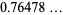 |
(6) |
(OEIS A091589), and
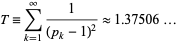 |
(7) |
(OEIS A086242; Finch 2003) is a convergent prime sum. The coefficients 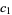 and
and 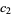 are given by the sums
are given by the sums
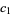 |
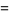 |
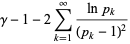 |
(8) |
 |
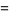 |
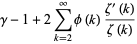 |
(9) |
 |
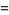 |
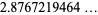 |
(10) |
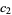 |
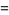 |
![-gamma_1-(gamma-1)[gamma-2sum_(k=1)^(infty)(lnp_k)/((p_k-1)^2)]-2sum_(k=1)^(infty)(p_k(lnp_k)^2)/((p_k-1)^3)](https://mathworld.wolfram.com/images/equations/PrimeFactor/Inline79.gif) |
(11) |
 |
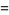 |
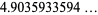 |
(12) |
(Diaconis 1976, Knuth 2000, Diaconis 2002, Finch 2003, Knuth 2003), where
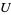 |
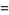 |
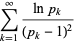 |
(13) |
 |
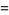 |
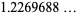 |
(14) |
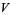 |
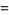 |
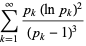 |
(15) |
 |
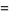 |
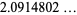 |
(16) |
(Finch 2003).
Similarly, if 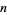 is chosen at random between 1 and
is chosen at random between 1 and  , then the probability that
, then the probability that
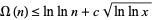 |
(17) |
approaches
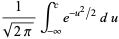 |
(18) |
as 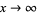 (Knuth 1998, p. 384). In addition, the average value
(Knuth 1998, p. 384). In addition, the average value 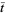 of
of 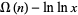 for
for 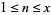 approaches
approaches 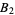 (Erdős and Kac 1940; Hardy and Wright 1979; Knuth 1998, p. 384)
(Erdős and Kac 1940; Hardy and Wright 1979; Knuth 1998, p. 384)

The average order of 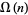 is
is
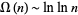 |
(19) |
(Hardy 1999, p. 51). More precisely,
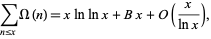 |
(20) |
for appropriate constants 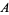 and
and 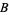 (Hardy and Ramanujan 1917; Hardy and Wright 1979, p. 355; Hardy 1999, p. 57), where
(Hardy and Ramanujan 1917; Hardy and Wright 1979, p. 355; Hardy 1999, p. 57), where 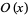 is asymptotic notation.
is asymptotic notation.
REFERENCES:
Conway, J. H.; Dietrich, H.; O'Brien, E. A. "Counting Groups: Gnus, Moas, and Other Exotica." Math. Intell. 30, 6-18, 2008.
Diaconis, P. "Asymptotic Expansions for the Mean and Variance of the Number of Prime Factors of a Number 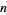 ." Dept. Statistics Tech. Report 96, Stanford, CA: Stanford University, 1976.
." Dept. Statistics Tech. Report 96, Stanford, CA: Stanford University, 1976.
Diaconis, P. "G. H. Hardy and Probability???" Bull. London Math. Soc. 34, 385-402, 2002.
Erdős, P. and Kac, M. "The Gaussian Law of Errors in the Theory of Additive Number Theoretic Functions." Amer. J. Math. 26, 738-742, 1940.
Finch, S. "Two Asymptotic Series." December 10, 2003. https://algo.inria.fr/bsolve/.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Ramanujan, S. Quart. J. Math. 48, 76-92, 1917.
Hardy, G. H. and Wright, E. M. §22.11 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 384, 1998.
Knuth, D. E. Selected Papers on Analysis of Algorithms. Stanford, CA: CSLI Publications, pp. 338-339, 2000.
Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. 327, 2000.
Sloane, N. J. A. Sequences A001222/M0094, A001221/M0056, A030059, A083342, A086242, and A091589 in "The On-Line Encyclopedia of Integer Sequences."
Turán, P. "On a Theorem of Hardy and Ramanujan." J. London Math. Soc. 9, 274-276, 1934.
Turán, P. "Über einige Verallgemeinerungen eines Satzes von Hardy und Ramanujan." J. London Math. Soc. 11, 125-133, 1936.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















