
Sieve of Eratosthenes
 المؤلف:
Conway, J. H. and Guy, R. K.
المؤلف:
Conway, J. H. and Guy, R. K.
 المصدر:
The Book of Numbers. New York: Springer-Verlag
المصدر:
The Book of Numbers. New York: Springer-Verlag
 الجزء والصفحة:
...
الجزء والصفحة:
...
 2-9-2020
2-9-2020
 2345
2345
Sieve of Eratosthenes

An algorithm for making tables of primes. Sequentially write down the integers from 2 to the highest number 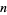 you wish to include in the table. Cross out all numbers
you wish to include in the table. Cross out all numbers 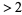 which are divisible by 2 (every second number). Find the smallest remaining number
which are divisible by 2 (every second number). Find the smallest remaining number 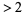 . It is 3. So cross out all numbers
. It is 3. So cross out all numbers 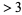 which are divisible by 3 (every third number). Find the smallest remaining number
which are divisible by 3 (every third number). Find the smallest remaining number 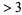 . It is 5. So cross out all numbers
. It is 5. So cross out all numbers 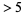 which are divisible by 5 (every fifth number).
which are divisible by 5 (every fifth number).
Continue until you have crossed out all numbers divisible by 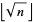 , where
, where 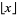 is the floor function. The numbers remaining are prime. This procedure is illustrated in the above diagram which sieves up to 50, and therefore crosses out composite numbers up to
is the floor function. The numbers remaining are prime. This procedure is illustrated in the above diagram which sieves up to 50, and therefore crosses out composite numbers up to 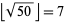 . If the procedure is then continued up to
. If the procedure is then continued up to 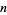 , then the number of cross-outs gives the number of distinct prime factors of each number.
, then the number of cross-outs gives the number of distinct prime factors of each number.
The sieve of Eratosthenes can be used to compute the prime counting function as
which is essentially an application of the inclusion-exclusion principle (Havil 2003, pp. 171-172).
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 127-130, 1996.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 100-101, 2004.
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 38-42, 2000.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, pp. 79-80, 1984.
Havil, J. "The Sieve of Eratosthenes." §15.5 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 171-172, 2003.
Haddon, M. The Curious Incident of the Dog in the Night-Time. New York: Vintage, pp. 11-12, 2003.
Nagell, T. "General Remarks. The Sieve of Eratosthenes." §15 in Introduction to Number Theory. New York: Wiley, pp. 51-54, 1951.
Pappas, T. The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 100-101, 1989.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 20-21, 1996.
Séroul, R. "The Sieve of Eratosthenes." §8.6 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 169-175, 2000.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 132, 2002.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


