

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Fermat,s Little Theorem
المؤلف:
Ball, W. W. R. and Coxeter, H. S. M.
المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover
الجزء والصفحة:
...
1-9-2020
2850
Fermat's Little Theorem
If 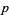 is a prime number and
is a prime number and 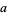 is a natural number, then
is a natural number, then
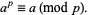 |
(1) |
Furthermore, if  (
( does not divide
does not divide 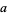 ), then there exists some smallest exponent
), then there exists some smallest exponent  such that
such that
 |
(2) |
and 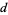 divides
divides  . Hence,
. Hence,
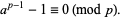 |
(3) |
The theorem is sometimes also simply known as "Fermat's theorem" (Hardy and Wright 1979, p. 63).
This is a generalization of the Chinese hypothesis and a special case of Euler's totient theorem. It is sometimes called Fermat's primality test and is a necessary but not sufficient test for primality. Although it was presumably proved (but suppressed) by Fermat, the first proof was published by Euler in 1749. It is unclear when the term "Fermat's little theorem" was first used to describe the theorem, but it was used in a German textbook by Hensel (1913) and appears in Mac Lane (1940) and Kaplansky (1945).
The theorem is easily proved using mathematical induction on  . Suppose
. Suppose  (i.e.,
(i.e.,  divides
divides  ). Then examine
). Then examine
 |
(4) |
From the binomial theorem,
 |
(5) |
Rewriting,
 |
(6) |
But  divides the right side, so it also divides the left side. Combining with the induction hypothesis gives that
divides the right side, so it also divides the left side. Combining with the induction hypothesis gives that  divides the sum
divides the sum
![[(a+1)^p-a^p-1]+(a^p-a)=(a+1)^p-(a+1),](https://mathworld.wolfram.com/images/equations/FermatsLittleTheorem/NumberedEquation7.gif) |
(7) |
as assumed, so the hypothesis is true for any  . The theorem is sometimes called Fermat's simple theorem. Wilson's theorem follows as a corollary of Fermat's little theorem.
. The theorem is sometimes called Fermat's simple theorem. Wilson's theorem follows as a corollary of Fermat's little theorem.
Fermat's little theorem shows that, if  is prime, there does not exist a base
is prime, there does not exist a base  with
with  such that
such that  possesses a nonzero residue modulo
possesses a nonzero residue modulo  . If such base
. If such base  exists,
exists,  is therefore guaranteed to be composite. However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that
is therefore guaranteed to be composite. However, the lack of a nonzero residue in Fermat's little theorem does not guarantee that  is prime. The property of unambiguously certifying composite numbers while passing some primes make Fermat's little theorem a compositeness test which is sometimes called the Fermat compositeness test. A number satisfying Fermat's little theorem for some nontrivial base and which is not known to be composite is called a probable prime.
is prime. The property of unambiguously certifying composite numbers while passing some primes make Fermat's little theorem a compositeness test which is sometimes called the Fermat compositeness test. A number satisfying Fermat's little theorem for some nontrivial base and which is not known to be composite is called a probable prime.
Composite numbers known as Fermat pseudoprimes (or sometimes simply "pseudoprimes") have zero residue for some  s and so are not identified as composite. Worse still, there exist numbers known as Carmichael numbers (the smallest of which is 561) which give zero residue for any choice of the base
s and so are not identified as composite. Worse still, there exist numbers known as Carmichael numbers (the smallest of which is 561) which give zero residue for any choice of the base  relatively prime to
relatively prime to  . However, Fermat's little theorem converse provides a criterion for certifying the primality of a number. A table of the smallest pseudoprimes
. However, Fermat's little theorem converse provides a criterion for certifying the primality of a number. A table of the smallest pseudoprimes  for the first 100 bases
for the first 100 bases  follows (OEIS A007535; Beiler 1966, p. 42 with typos corrected).
follows (OEIS A007535; Beiler 1966, p. 42 with typos corrected).
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 2 | 341 | 22 | 69 | 42 | 205 | 62 | 63 | 82 | 91 |
| 3 | 91 | 23 | 33 | 43 | 77 | 63 | 341 | 83 | 105 |
| 4 | 15 | 24 | 25 | 44 | 45 | 64 | 65 | 84 | 85 |
| 5 | 124 | 25 | 28 | 45 | 76 | 65 | 112 | 85 | 129 |
| 6 | 35 | 26 | 27 | 46 | 133 | 66 | 91 | 86 | 87 |
| 7 | 25 | 27 | 65 | 47 | 65 | 67 | 85 | 87 | 91 |
| 8 | 9 | 28 | 45 | 48 | 49 | 68 | 69 | 88 | 91 |
| 9 | 28 | 29 | 35 | 49 | 66 | 69 | 85 | 89 | 99 |
| 10 | 33 | 30 | 49 | 50 | 51 | 70 | 169 | 90 | 91 |
| 11 | 15 | 31 | 49 | 51 | 65 | 71 | 105 | 91 | 115 |
| 12 | 65 | 32 | 33 | 52 | 85 | 72 | 85 | 92 | 93 |
| 13 | 21 | 33 | 85 | 53 | 65 | 73 | 111 | 93 | 301 |
| 14 | 15 | 34 | 35 | 54 | 55 | 74 | 75 | 94 | 95 |
| 15 | 341 | 35 | 51 | 55 | 63 | 75 | 91 | 95 | 141 |
| 16 | 51 | 36 | 91 | 56 | 57 | 76 | 77 | 96 | 133 |
| 17 | 45 | 37 | 45 | 57 | 65 | 77 | 247 | 97 | 105 |
| 18 | 25 | 38 | 39 | 58 | 133 | 78 | 341 | 98 | 99 |
| 19 | 45 | 39 | 95 | 59 | 87 | 79 | 91 | 99 | 145 |
| 20 | 21 | 40 | 91 | 60 | 341 | 80 | 81 | 100 | 153 |
| 21 | 55 | 41 | 105 | 61 | 91 | 81 | 85 |
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 61, 1987.
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 141-142, 1996.
Courant, R. and Robbins, H. "Fermat's Theorem." §2.2 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 37-38, 1996.
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 118-125, 2000.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Hensel, K. Zahlentheorie. Berlin: G. J. Göschen, 1913.
Kaplansky, I. "Lucas's Tests for Mersenne Numbers." Amer. Math. Monthly 52, 188-190, 1945.
Mac Lane, S. "Modular Fields." Amer. Math. Monthly 47, 259-274, 1940.
Nagell, T. "Fermat's Theorem and Its Generalization by Euler." §21 in Introduction to Number Theory. New York: Wiley, pp. 71-73, 1951.
Séroul, R. "The Theorems of Fermat and Euler." §2.8 in Programming for Mathematicians. Berlin: Springer-Verlag, p. 15, 2000.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 20, 1993.
Sloane, N. J. A. Sequence A007535/M5440 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















