
Totient Valence Function
 المؤلف:
Conway, J. H. and Guy, R. K.
المؤلف:
Conway, J. H. and Guy, R. K.
 المصدر:
The Book of Numbers. New York: Springer-Verlag
المصدر:
The Book of Numbers. New York: Springer-Verlag
 الجزء والصفحة:
...
الجزء والصفحة:
...
 28-8-2020
28-8-2020
 2291
2291
Totient Valence Function
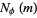 is the number of integers
is the number of integers 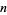 for which the totient function
for which the totient function 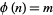 , also called the multiplicity of
, also called the multiplicity of 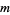 (Guy 1994). Erdős (1958) proved that if a multiplicity occurs once, it occurs infinitely often.
(Guy 1994). Erdős (1958) proved that if a multiplicity occurs once, it occurs infinitely often.
The values of 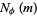 for
for 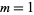 , 2, ... are 2, 3, 0, 4, 0, 4, 0, 5, 0, 2, 0, 6, ... (OEIS A014197), and the nonzero values are 2, 3, 4, 4, 5, 2, 6, 6, 4, 5, 2, 10, 2, 2, 7, 8, 9, ... (OEIS A058277), which occur for
, 2, ... are 2, 3, 0, 4, 0, 4, 0, 5, 0, 2, 0, 6, ... (OEIS A014197), and the nonzero values are 2, 3, 4, 4, 5, 2, 6, 6, 4, 5, 2, 10, 2, 2, 7, 8, 9, ... (OEIS A058277), which occur for 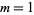 , 2, 4, 6, 8, 10, 12, 16, 18, 20, ... (OEIS A002202). The table below lists values for
, 2, 4, 6, 8, 10, 12, 16, 18, 20, ... (OEIS A002202). The table below lists values for 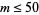 .
.
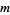 |
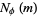 |
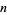 such that such that 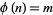 |
| 1 |
2 |
1, 2 |
| 2 |
3 |
3, 4, 6 |
| 4 |
4 |
5, 8, 10, 12 |
| 6 |
4 |
7, 9, 14, 18 |
| 8 |
5 |
15, 16, 20, 24, 30 |
| 10 |
2 |
11, 22 |
| 12 |
6 |
13, 21, 26, 28, 36, 42 |
| 16 |
6 |
17, 32, 34, 40, 48, 60 |
| 18 |
4 |
19, 27, 38, 54 |
| 20 |
5 |
25, 33, 44, 50, 66 |
| 22 |
2 |
23, 46 |
| 24 |
10 |
35, 39, 45, 52, 56, 70, 72, 78, 84, 90 |
| 28 |
2 |
29, 58 |
| 30 |
2 |
31, 62 |
| 32 |
7 |
51, 64, 68, 80, 96, 102, 120 |
| 36 |
8 |
37, 57, 63, 74, 76, 108, 114, 126 |
| 40 |
9 |
41, 55, 75, 82, 88, 100, 110, 132, 150 |
| 42 |
4 |
43, 49, 86, 98 |
| 44 |
3 |
69, 92, 138 |
| 46 |
2 |
47, 94 |
| 48 |
11 |
65, 104, 105, 112, 130, 140, 144, 156, 168, 180, 210 |
The smallest 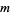 such that
such that 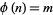 has exactly 2, 3, 4, ... solutions are given by 1, 2, 4, 8, 12, 32, 36, 40, 24, ... (OEIS A007374). Including Carmichael's conjecture that
has exactly 2, 3, 4, ... solutions are given by 1, 2, 4, 8, 12, 32, 36, 40, 24, ... (OEIS A007374). Including Carmichael's conjecture that 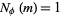 has no solutions, the smallest
has no solutions, the smallest 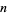 such that
such that 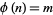 has exactly 0, 1, 2, 3, 4, ... solutions are given by 3, 0, 1, 2, 4, 8, 12, 32, 36, 40, 24, ... (OEIS A014573). A table listing the first value of
has exactly 0, 1, 2, 3, 4, ... solutions are given by 3, 0, 1, 2, 4, 8, 12, 32, 36, 40, 24, ... (OEIS A014573). A table listing the first value of 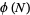 with multiplicities up to 100 follows.
with multiplicities up to 100 follows.
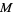 |
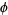 |
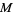 |
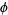 |
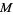 |
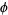 |
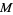 |
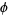 |
| 0 |
3 |
26 |
2560 |
51 |
4992 |
76 |
21840 |
| 2 |
1 |
27 |
384 |
52 |
17640 |
77 |
9072 |
| 3 |
2 |
28 |
288 |
53 |
2016 |
78 |
38640 |
| 4 |
4 |
29 |
1320 |
54 |
1152 |
79 |
9360 |
| 5 |
8 |
30 |
3696 |
55 |
6000 |
80 |
81216 |
| 6 |
12 |
31 |
240 |
56 |
12288 |
81 |
4032 |
| 7 |
32 |
32 |
768 |
57 |
4752 |
82 |
5280 |
| 8 |
36 |
33 |
9000 |
58 |
2688 |
83 |
4800 |
| 9 |
40 |
34 |
432 |
59 |
3024 |
84 |
4608 |
| 10 |
24 |
35 |
7128 |
60 |
13680 |
85 |
16896 |
| 11 |
48 |
36 |
4200 |
61 |
9984 |
86 |
3456 |
| 12 |
160 |
37 |
480 |
62 |
1728 |
87 |
3840 |
| 13 |
396 |
38 |
576 |
63 |
1920 |
88 |
10800 |
| 14 |
2268 |
39 |
1296 |
64 |
2400 |
89 |
9504 |
| 15 |
704 |
40 |
1200 |
65 |
7560 |
90 |
18000 |
| 16 |
312 |
41 |
15936 |
66 |
2304 |
91 |
23520 |
| 17 |
72 |
42 |
3312 |
67 |
22848 |
92 |
39936 |
| 18 |
336 |
43 |
3072 |
68 |
8400 |
93 |
5040 |
| 19 |
216 |
44 |
3240 |
69 |
29160 |
94 |
26208 |
| 20 |
936 |
45 |
864 |
70 |
5376 |
95 |
27360 |
| 21 |
144 |
46 |
3120 |
71 |
3360 |
96 |
6480 |
| 22 |
624 |
47 |
7344 |
72 |
1440 |
97 |
9216 |
| 23 |
1056 |
48 |
3888 |
73 |
13248 |
98 |
2880 |
| 24 |
1760 |
49 |
720 |
74 |
11040 |
99 |
26496 |
| 25 |
360 |
50 |
1680 |
75 |
27720 |
100 |
34272 |
It is thought that 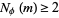 (i.e., the totient valence function never takes on the value 1), but this has not been proven. This assertion is called Carmichael's totient function conjecture and is equivalent to the statement that for all
(i.e., the totient valence function never takes on the value 1), but this has not been proven. This assertion is called Carmichael's totient function conjecture and is equivalent to the statement that for all 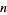 , there exists
, there exists 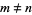 such that
such that 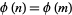 (Ribenboim 1996, pp. 39-40). Any counterexample must have more than
(Ribenboim 1996, pp. 39-40). Any counterexample must have more than 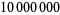 digits (Schlafly and Wagon 1994; erroneously given as
digits (Schlafly and Wagon 1994; erroneously given as 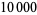 in Conway and Guy 1996).
in Conway and Guy 1996).
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 155, 1996.
Erdős, P. "Some Remarks on Euler's 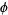 -Function." Acta Math. 4, 10-19, 1958.
-Function." Acta Math. 4, 10-19, 1958.
Ford, K. "The Distribution of Totients." Ramanujan J. 2, 67-151, 1998.
Ford, K. "The Distribution of Totients, Electron. Res. Announc. Amer. Math. Soc. 4, 27-34, 1998.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 94, 1994.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Schlafly, A. and Wagon, S. "Carmichael's Conjecture on the Euler Function is Valid Below 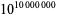 ." Math. Comput. 63, 415-419, 1994.
." Math. Comput. 63, 415-419, 1994.
Sloane, N. J. A. Sequences A002202/M0987, A007374/M1093, A014197, A014573, A058277, and A082695 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


