The Riemann-Siegel formula is a formula discovered (but not published) by Riemann for computing an asymptotic formula for the Riemann-Siegel function 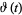. The formula was subsequently discovered in an archive of Riemann's papers by C. L. Siegel (Edwards 2001, p. 136; Derbyshire 2004, pp. 257 and 263) and published by Siegel in 1932.

The Riemann-Siegel formula states that

(1)

where

			(2)
			(3)
		{exp[i(ln(t/(2pi))-1/2t-1/8pi-theta(t))]×[y^0][(sum_(j=0)^(infty)A_j(y)omega^j)(sum_(j=0)^(infty)(psi^((j))(p))/(j!)y^j)]}" src="https://mathworld.wolfram.com/images/equations/Riemann-SiegelFormula/Inline10.gif" style="height:49px; width:472px" />	(4)
			(5)
			(6)
			(7)

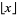 is the floor function (Edwards 2001), and  is coefficient notation. The first few terms 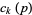 are given by

			(8)
			(9)
			(10)
			(11)
			(12)
			(13)

The numerators and denominators are 1, 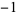, 1, 1, 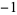, , 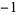, 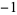1, 19, 11, 1, 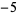, , 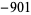... (OEIS A050276) and 1, 96, 64, 18432, 64, 3840, 5308416, 128, ... (OEIS A050277), respectively.

It is based on evaluation of the integral

			(14)
			(15)

also denoted 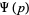, where  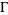is a line segment of slope 1, directed from upper right to lower left, which crosses the imaginary axis between 0 and  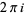(Edwards 2001, p. 147).

Another formula ascribed to Riemann and Siegel is the one presented by Riemann in his groundbreaking 1859 paper,

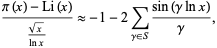(16)

where 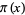 is the prime counting function,  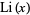is the logarithmic integral, and  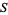is the set of  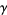such that  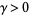and 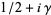 is a (nontrivial) zero of the Riemann zeta function 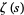. Here, the left side is the overcount of  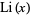as an estimator for the prime counting function normalized by the apparent size of the error term (Borwein and Bailey 2003, p. 68).

REFERENCES:

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 68, 2003.

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Edwards, H. M. "The Riemann-Siegel Formula." Ch. 7 in Riemann's Zeta Function. New York: Dover, pp. 136-170, 2001.

Granville, A. and Martin, G. "Prime Number Races." Aug. 24, 2004. https://www.arxiv.org/abs/math.NT/0408319.

Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859. Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972.

Sloane, N. J. A. Sequences A050276 and A050277 in "The On-Line Encyclopedia of Integer Sequences."