A Sierpiński number of the second kind is a number 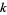 satisfying Sierpiński's composite number theorem, i.e., a Proth number  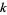such that  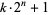is composite for every .

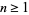The smallest known example is 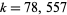, proved in 1962 by J. Selfridge, but the fate of a number of smaller candidates remains to be determined before this number can be established as the smallest such number. As of 1996, 35 candidates remained (Ribenboim 1996, p. 358), a number which had been reduced to 17 by the beginning of 2002 (Peterson 2003).

In March 2002, L. K. Helm and D. A. Norris began a distributed computing effort dubbed "seventeen or bust" to eliminate the remaining candidates. With the aid of collaborators across the globe, this number was reduced to 12 as of December 2003 (Peterson 2003, Helm and Norris). The following table summarizes numbers subsequently found to be prime by "seventeen or bust," leaving only five candidates remaining as of November 2016.

date	participant	number
Dec. 6, 2003
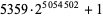Jun. 8, 2005	D. Gordon
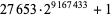Oct. 15, 2005	R. Hassler
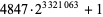May 5, 2007	K. Agafonov
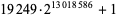Oct. 30, 2007	S. Sunde
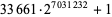Nov. 6, 2016	P. Szabolcs

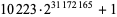The following table lists the known primes together with the only remaining candidates which, as Jan. 2008, are the six numbers 10223, 21181, 22699, 24737, 55459, and 67607. A list of primes found by the project is also maintained by Caldwell (https://primes.utm.edu/bios/page.php?id=429).

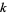	prime	digits	Caldwell
4847		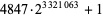999744	https://primes.utm.edu/primes/page.php?id=75994
5359		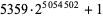1521561	https://primes.utm.edu/primes/page.php?id=67719
10223		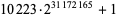9383761	https://primes.utm.edu/primes/page.php?id=122473
19249		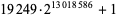3918990	https://primes.utm.edu/primes/page.php?id=80385
21181
22699
24737
27653		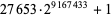2759677	https://primes.utm.edu/primes/page.php?id=74836
28433		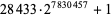2357207	https://primes.utm.edu/primes/page.php?id=73145
33661		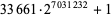2116617	https://primes.utm.edu/primes/page.php?id=82804
44131		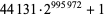299823	https://primes.utm.edu/primes/page.php?id=62867
46157		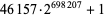210186	https://primes.utm.edu/primes/page.php?id=62865
54767		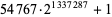402569	https://primes.utm.edu/primes/page.php?id=62869
55459
65567		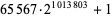305190	https://primes.utm.edu/primes/page.php?id=62866
67607
69109		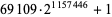348431	https://primes.utm.edu/primes/page.php?id=62868

Consider now restricting Sierpiński numbers of the second kind to those with prime 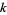. The smallest proved prime Sierpiński number is 271129. A distributed computing project to find examples of  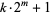that are prime with  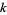smaller than the proven lower limit is currently underway (Caldwell). Note that the smallest candidates include three prime candidates from the "seventeen or bust" list: 10223, 22699, 67607. A list of primes found by the project is maintained by Caldwell (https://primes.utm.edu/bios/page.php?id=564).

Let 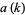 be smallest  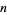for which  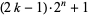is prime, then the first few values are 0, 1, 1, 2, 1, 1, 2, 1, 3, 6, 1, 1, 2, 2, 1, 8, 1, 1, 2, 1, 1, 2, 2, 583, ... (OEIS A046067). The second smallest  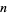are given by 1, 2, 3, 4, 2, 3, 8, 2, 15, 10, 4, 9, 4, 4, 3, 60, 6, 3, 4, 2, 11, 6, 9, 1483, ... (OEIS A046068). Quite large  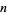can be required to obtain the first prime even for small 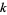. For example, the smallest prime of the form  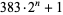is .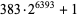

There are an infinite number of Sierpiński numbers which are prime.

The smallest odd 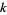 such that  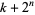is composite for all  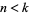are 773, 2131, 2491, 4471, 5101, ... (OEIS A033919).

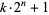 is always composite for  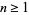and Gaussian integers 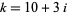, , 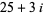and 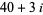. (E. Pegg Jr., pers. comm., Feb. 6, 2003; Broadhurst 2005).

REFERENCES:

Baillie, R.; Cormack, G.; and Williams, H. C. "The Problem of Sierpinski Concerning 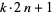." Math. Comput. 37, 229-231, 1981.

Ballinger, R. "The Sierpinski Problem: Definition and Status." https://www.prothsearch.net/sierp.html.

Broadhurst, D. "Might Jean Complexify SoB?" primeform group posting. Oct. 30, 2005. https://groups.yahoo.com/group/primeform/message/6620/.

Caldwell, C. "The Prime Sierpinski Problem." https://primes.utm.edu/bios/page.php?id=564.

Caldwell, C. "Seventeen or Bust." https://primes.utm.edu/bios/page.php?id=429.

Buell, D. A. and Young, J. "Some Large Primes and the Sierpiński Problem." SRC Tech. Rep. 88004, Supercomputing Research Center, Lanham, MD, 1988.

Helm, L. Press release upon discovery of 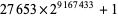. June 15, 2005. https://www.seventeenorbust.com/documents/press-061505.mhtml.

Helm, L. Press release upon discovery of 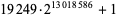. May 5, 2007. https://www.seventeenorbust.com/documents/press-050507.mhtml.

Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem." https://www.seventeenorbust.com/.

Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem--Project Statistics." https://www.seventeenorbust.com/stats/.

Jaeschke, G. "On the Smallest 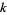 such that  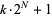are Composite." Math. Comput. 40, 381-384, 1983.

Jaeschke, G. Corrigendum to "On the Smallest 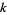 such that  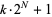are Composite." Math. Comput. 45, 637, 1985.

Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 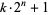." Math. Comput. 41, 661-673, 1983.

Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 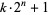, II." In prep.

Peterson, I. "MathTrek: A Remarkable Dearth of Primes." Jan. 13, 2003. https://www.sciencenews.org/20030111/mathtrek.asp.

"The Prime Sierpinski Project." https://www.mersenneforum.org/showthread.php?t=2665.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 357-359, 1996.

Sierpiński, W. "Sur un problème concernant les nombres 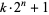." Elem. d. Math. 15, 73-74, 1960.

Sloane, N. J. A. Sequences A033919, A046067, and A046068 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

مجموعة العميد التربوية تعقد اجتماعًا لمناقشة الاستعدادات الخاصة بالموسم التدريبي الصيفي

قسم الإعلام ينظم ورشة تدريبية حول تطبيق (إعلامي) لعدد من منتسبي قسم حفظ النظام

قسم الشؤون الخدمية ينفذ حملة لتنظيف الشوارع المحيطة بصحن مرقد أبي الفضل العباس (عليه السلام)

وفد العتبة العباسية المقدسة يزور شعبة الإعداد البدني للاطّلاع على برنامج تأهيل المنتسبين الجدد

المزيد

الآخبار الصحية

ماذا يحدث إذا تناولنا الطعام مرة واحدة فقط في اليوم

اكتشاف عوامل خطر غير متوقعة لمرض الكبد الدهني

فيروس هانتا والسفينة الموبوءة.. تحديث من الصحة العالمية

طبيب يحسم الجدل السجائر الإلكترونية وعلاقتها بالسرطان

المزيد

الآخبار التكنلوجية

لأول مرة في الولايات المتحدة.. تشغيل مفاعل مصغر نووي يغذي الذكاء الاصطناعي بالطاقة

الكشف عن تفاصيل أول عملية ناجحة لاستعادة انتاج الحيوانات المنوية

أطلس يكشف خفايا الجسم البشري بدقة أرفع بـ50 مرة من شعر الإنسان

المتحف المصري الكبير يتحول إلى "أيقونة خضراء" بدعم ياباني

المزيد