Goldbach's original conjecture (sometimes called the "ternary" Goldbach conjecture), written in a June 7, 1742 letter to Euler, states "at least it seems that every number that is greater than 2 is the sum of three primes" (Goldbach 1742; Dickson 2005, p. 421). Note that Goldbach considered the number 1 to be a prime, a convention that is no longer followed. As re-expressed by Euler, an equivalent form of this conjecture (called the "strong" or "binary" Goldbach conjecture) asserts that all positive even integers  can be expressed as the sum of two primes. Two primes  such that  for  a positive integer are sometimes called a Goldbach partition (Oliveira e Silva).

According to Hardy (1999, p. 19), "It is comparatively easy to make clever guesses; indeed there are theorems, like 'Goldbach's Theorem,' which have never been proved and which any fool could have guessed." Faber and Faber offered a  prize to anyone who proved Goldbach's conjecture between March 20, 2000 and March 20, 2002, but the prize went unclaimed and the conjecture remains open.

Schnirelman (1939) proved that every even number can be written as the sum of not more than  primes (Dunham 1990), which seems a rather far cry from a proof for two primes! Pogorzelski (1977) claimed to have proven the Goldbach conjecture, but his proof is not generally accepted (Shanks 1985). The following table summarizes bounds  such that the strong Goldbach conjecture has been shown to be true for numbers .

bound	reference
	Desboves 1885
	Pipping 1938
	Stein and Stein 1965ab
	Granville et al. 1989
	Sinisalo 1993
	Deshouillers et al. 1998
	Richstein 1999, 2001
	Oliveira e Silva (Mar. 24, 2003)
	Oliveira e Silva (Oct. 3, 2003)
	Oliveira e Silva (Feb. 5, 2005)
	Oliveira e Silva (Dec. 30, 2005)
	Oliveira e Silva (Jul. 14, 2008)
	Oliveira e Silva (Apr. 2012)

The conjecture that all odd numbers  are the sum of three odd primes is called the "weak" Goldbach conjecture. Vinogradov (1937ab, 1954) proved that every sufficiently large odd number is the sum of three primes (Nagell 1951, p. 66; Guy 1994), and Estermann (1938) proved that almost all even numbers are the sums of two primes. Vinogradov's original "sufficiently large"  was subsequently reduced to  by Chen and Wang (1989). Chen (1973, 1978) also showed that all sufficiently large even numbers are the sum of a prime and the product of at most two primes (Guy 1994, Courant and Robbins 1996). More than two and a half centuries after the original conjecture was stated, the weak Goldbach conjecture was proved by Helfgott (2013, 2014).

A stronger version of the weak conjecture, namely that every odd number  can be expressed as the sum of a prime plus twice a prime is known as Levy's conjecture.

An equivalent statement of the Goldbach conjecture is that for every positive integer , there are primes  and  such that

where  is the totient function (e.g., Havil 2003, p. 115; Guy 2004, p. 160). (This follows immediately from  for  prime.) Erdős and Moser have considered dropping the restriction that  and  be prime in this equation as a possibly easier way of determining if such numbers always exist (Guy 1994, p. 105).

Other variants of the Goldbach conjecture include the statements that every even number  is the sum of two odd primes, and every integer  the sum of exactly three distinct primes.

Let  be the number of representations of an even number  as the sum of two primes. Then the "extended" Goldbach conjecture states that

where 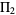 is the twin primes constant (Halberstam and Richert 1974).

REFERENCES:

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 64, 1987.

Caldwell, C. K. "Prime Links++." https://primes.utm.edu/links/theory/conjectures/Goldbach/.

Chen, J. R. "On the Representation of a Large Even Integer as the Sum of a Prime and the Product of at Most Two Primes." Sci. Sinica 16, 157-176, 1973.

Chen, J. R. "On the Representation of a Large Even Integer as the Sum of a Prime and the Product of at Most Two Primes, II." Sci. Sinica 21, 421-430, 1978.

Chen, J. R. and Wang, T.-Z. "On the Goldbach Problem." Acta Math. Sinica 32, 702-718, 1989.

Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 30-31, 1996.

Deshouillers, J.-M.; te Riele, H. J. J.; and Saouter, Y. "New Experimental Results Concerning The Goldbach Conjecture." In Algorithmic Number Theory: Proceedings of the 3rd International Symposium (ANTS-III) held at Reed College, Portland, OR, June 21-25, 1998 (Ed. J. P. Buhler). Berlin: Springer-Verlag, pp. 204-215, 1998.

Devlin, K. Mathematics: The New Golden Age, rev. ed. New York: Columbia University Press, 1999.

Dickson, L. E. "Goldbach's Empirical Theorem: Every Integer is a Sum of Two Primes." In History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 421-424, 2005.

Doxiadis, A. Uncle Petros and Goldbach's Conjecture. Faber & Faber, 2001.

Dunham, W. Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, p. 83, 1990.

Estermann, T. "On Goldbach's Problem: Proof that Almost All Even Positive Integers are Sums of Two Primes." Proc. London Math. Soc. Ser. 2 44, 307-314, 1938.

Faber and Faber. "$1,000,000 Challenge to Prove Goldbach's Conjecture." Archived at https://web.archive.org/web/20020803035741/www.faber.co.uk/faber/million_dollar.asp.

Goldbach, C. Letter to L. Euler, June 7, 1742.

Granville, A.; van der Lune, J.; and te Riele, H. J. J. "Checking the Goldbach Conjecture on a Vector Computer." In Number Theory and Applications: Proceedings of the NATO Advanced Study Institute held in Banff, Alberta, April 27-May 5, 1988 (Ed. R. A. Mollin). Dordrecht, Netherlands: Kluwer, pp. 423-433, 1989.

Guy, R. K. "Goldbach's Conjecture." §C1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 105-107, 1994.

Guy, R. K. Unsolved Problems in Number Theory, 3rd ed. New York: Springer-Verlag, 2004.

Halberstam, H. and Richert, H.-E. Sieve Methods. New York: Academic Press, 1974.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Hardy, G. H. and Littlewood, J. E. "Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes." Acta Math. 44, 1-70, 1923.

Hardy, G. H. and Littlewood, J. E. "Some Problems of Partitio Numerorum (V): A Further Contribution to the Study of Goldbach's Problem." Proc. London Math. Soc. Ser. 2 22, 46-56, 1924.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, p. 19, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Helfgott, H. A. "The Ternary Goldbach Conjecture." Gac. R. Soc. Mat. Esp. 16, 709-726, 2013.

Helfgott, H. A. "The Ternary Goldbach Conjecture Is True." Jan. 17, 2014. https://arxiv.org/pdf/1312.7748.pdf.

Nagell, T. Introduction to Number Theory. New York: Wiley, p. 66, 1951.

Oliveira e Silva, T. "Goldbach Conjecture Verification." https://www.ieeta.pt/~tos/goldbach.html.

Oliveira e Silva, T. "Verification of the Goldbach Conjecture Up to 2*10^16." Mar. 24, 2003a. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0303&L=nmbrthry&P=2394.

Oliveira e Silva, T. "Verification of the Goldbach Conjecture Up to 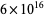." Oct. 3, 2003b. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0310&L=nmbrthry&P=168.

Oliveira e Silva, T. "New Goldbach Conjecture Verification Limit." Feb. 5, 2005a. https://listserv.nodak.edu/cgi-bin/wa.exe?A1=ind0502&L=nmbrthry#9.

Oliveira e Silva, T. "Goldbach Conjecture Verification." Dec. 30, 2005b. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0512&L=nmbrthry&T=0&P=3233.

Peterson, I. "Prime Conjecture Verified to New Heights." Sci. News 158, 103, Aug. 12, 2000.

Pipping, N. "Die Goldbachsche Vermutung und der Goldbach-Vinogradovsche Satz." Acta. Acad. Aboensis, Math. Phys. 11, 4-25, 1938.

Pogorzelski, H. A. "Goldbach Conjecture." J. reine angew. Math. 292, 1-12, 1977.

Richstein, J. "Verifying the Goldbach Conjecture up to 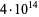." Presented at Canadian Number Theory Association, Winnipeg/Canada June 20-24, 1999.

Richstein, J. "Verifying the Goldbach Conjecture up to 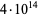." Math. Comput. 70, 1745-1750, 2001.

Schnirelman, L. G. Uspekhi Math. Nauk 6, 3-8, 1939.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 30-31 and 222, 1985.

Sinisalo, M. K. "Checking the Goldbach Conjecture up to 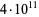." Math. Comput. 61, 931-934, 1993.

Stein, M. L. and Stein, P. R. "New Experimental Results on the Goldbach Conjecture." Math. Mag. 38, 72-80, 1965a.

Stein, M. L. and Stein, P. R. "Experimental Results on Additive 2 Bases." BIT 38, 427-434, 1965b.

Vinogradov, I. M. "Representation of an Odd Number as a Sum of Three Primes." Comptes rendus (Doklady) de l'Académie des Sciences de l'U.R.S.S. 15, 169-172, 1937a.

Vinogradov, I. "Some Theorems Concerning the Theory of Primes." Recueil Math. 2, 179-195, 1937b.

Vinogradov, I. M. The Method of Trigonometrical Sums in the Theory of Numbers. London: Interscience, p. 67, 1954.

Woon, M. S. C. "On Partitions of Goldbach's Conjecture" 4 Oct 2000. https://arxiv.org/abs/math.GM/0010027.

Wang, Y. Goldbach Conjecture. Singapore: World Scientific, 1984.