
Elliptic Discriminant
 المؤلف:
المرجع الالكتروني للمعلوماتيه
المؤلف:
المرجع الالكتروني للمعلوماتيه
 المصدر:
www.almerja.com
المصدر:
www.almerja.com
 الجزء والصفحة:
...
الجزء والصفحة:
...
 6-7-2020
6-7-2020
 1261
1261
Elliptic Discriminant
An elliptic curve is the set of solutions to an equation of the form
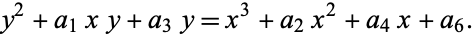 |
(1)
|
By changing variables, 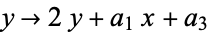 , assuming the field characteristic is not 2, the equation becomes
, assuming the field characteristic is not 2, the equation becomes
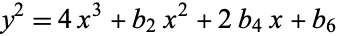 |
(2)
|
where
Define also the quantity
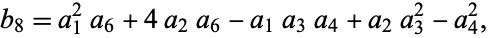 |
(6)
|
then the discriminant is given by
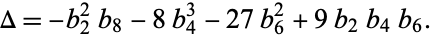 |
(7)
|
The discriminant depends on the choice of equations, and can change after a change of variables, unlike the j-invariant.
If the field characteristic is neither 2 or 3, then its equation can be written as
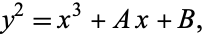 |
(8)
|
in which case, the discriminant is given by
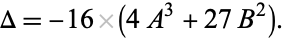 |
(9)
|
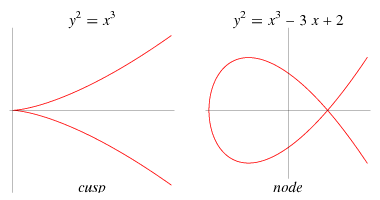
Algebraically, the discriminant is nonzero when the right-hand side has three distinct roots. In the classical case of an elliptic curve over the complex numbers, the discriminant has a geometric interpretation. If 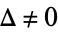 , then the elliptic curve is nonsingular and has curve genus 1, i.e., it is a torus. If
, then the elliptic curve is nonsingular and has curve genus 1, i.e., it is a torus. If 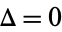 and
and 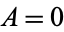 , then it has a cusp singularity, in which case there is one tangent direction at the singularity. If
, then it has a cusp singularity, in which case there is one tangent direction at the singularity. If 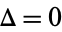 and
and 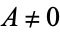 , then its singularity is called an ordinary double point (or node), in which case the singularity has two distinct tangent directions.
, then its singularity is called an ordinary double point (or node), in which case the singularity has two distinct tangent directions.
Note that the discriminant of an elliptic curve is not the same as the polynomial discriminant of the corresponding polynomial, but the two kinds of discriminants vanish for the same values of 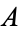 and
and 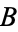 .
.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


