Leudesdorf Theorem
المؤلف:
Hardy, G. H. and Wright, E. M.
المصدر:
"A Theorem of Leudesdorf." §8.7 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press
الجزء والصفحة:
pp. 100-102
30-6-2020
1476
Leudesdorf Theorem
Let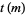 
denote the set of the 
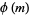numbers less than and relatively prime to 
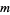, where 
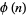is the totient function. Then if
 |
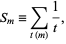(1)
|
then
![<span style=]() {S_m=0 (mod m^2) if 2m, 3m; S_m=0 (mod 1/3m^2) if 2m, 3|m; S_m=0 (mod 1/2m^2) 2|m, 3m, m not a power of 2; S_m=0 (mod 1/6m^2) if 2|m, 3|m; S_m=0 (mod 1/4m^2) if m=2^a. " src="https://mathworld.wolfram.com/images/equations/LeudesdorfTheorem/NumberedEquation2.gif" style="height:142px; width:306px" /> |
(2)
|
REFERENCES:
Hardy, G. H. and Wright, E. M. "A Theorem of Leudesdorf." §8.7 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 100-102, 1979.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
