The rational distance problem asks to find a geometric configuration satisfying given properties such that all distances along specific edges are rational numbers. (This is equivalent to having all edge lengths be integers, since the denominators of rational numbers can be cleared by multiplication.)

A cuboid whose edges and face diagonals are integers is called an Euler brick. It is not known if there exists a point in a unit square all of whose distances from the corners are rational, although J. H. Conway and M. Guy found an infinite numbers of solutions to the problem of three such distances being integers, which involves solving

where 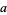, , 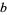and 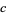 are the three distances and  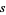is the side length of the square (Guy 1994, p. 181). There are infinitely many solutions of the corresponding problem of integer distances from the corners of an equilateral triangle (Guy 1994, p. 183).

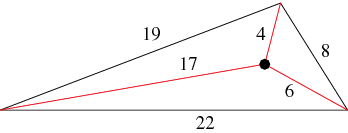
In 2001, E. Pegg found a small scalene triangle with side lengths 8, 22, and 19 possessing an internal point with distances 17, 6, and 4 from the respective vertices. This is equivalent to finding an integers-only solution of the equation for the six distances between vertices of a quadrilateral.

REFERENCES:

Guy, R. K. "Rational Distances from the Corner of a Square." §D19 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 181-185, 1994.

اخر الاخبار

اخبار العتبة العباسية المقدسة

مجموعة العميد التربوية تعقد اجتماعًا لمناقشة الاستعدادات الخاصة بالموسم التدريبي الصيفي

قسم الإعلام ينظم ورشة تدريبية حول تطبيق (إعلامي) لعدد من منتسبي قسم حفظ النظام

قسم الشؤون الخدمية ينفذ حملة لتنظيف الشوارع المحيطة بصحن مرقد أبي الفضل العباس (عليه السلام)

وفد العتبة العباسية المقدسة يزور شعبة الإعداد البدني للاطّلاع على برنامج تأهيل المنتسبين الجدد

المزيد

الآخبار الصحية

ماذا يحدث إذا تناولنا الطعام مرة واحدة فقط في اليوم

اكتشاف عوامل خطر غير متوقعة لمرض الكبد الدهني

فيروس هانتا والسفينة الموبوءة.. تحديث من الصحة العالمية

طبيب يحسم الجدل السجائر الإلكترونية وعلاقتها بالسرطان

المزيد

الآخبار التكنلوجية

لأول مرة في الولايات المتحدة.. تشغيل مفاعل مصغر نووي يغذي الذكاء الاصطناعي بالطاقة

الكشف عن تفاصيل أول عملية ناجحة لاستعادة انتاج الحيوانات المنوية

أطلس يكشف خفايا الجسم البشري بدقة أرفع بـ50 مرة من شعر الإنسان

المتحف المصري الكبير يتحول إلى "أيقونة خضراء" بدعم ياباني

المزيد