Consider a set {a_1,a_2,...,a_n}" src="https://mathworld.wolfram.com/images/equations/PostageStampProblem/Inline1.gif" style="height:15px; width:119px" /> of 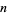 positive integer-denomination postage stamps sorted such that 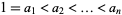. Suppose they are to be used on an envelope with room for no more than  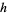stamps. 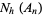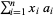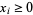The postage stamp problem then consists of determining the smallest integer  which cannot be represented by a linear combination  with  and .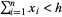

Without the latter restriction, this problem is known as the Frobenius problem or Frobenius postage stamp problem.

The number of consecutive possible postage amounts is given by

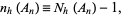(1)

where 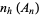 is called an 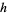-range.

Exact solutions exist for arbitrary 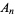 for 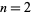 and 3. The  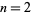solution is

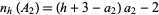(2)

for 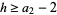. It is also known that

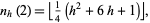(3)

(Stöhr 1955, Guy 1994), where 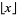 is the floor function, the first few values of which are 2, 4, 7, 10, 14, 18, 23, 28, 34, 40, ... (OEIS A014616; Guy 1994, p. 123).

Hofmeister (1968, 1983) showed that for ,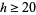

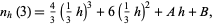(4)

where 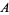 and 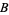 are functions of  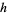(mod 9), and Mossige (1981, 1987) showed that

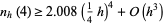(5)

(Guy 1994, p. 123).

Shallit (2002) proved that the (local) postage stamp problem is NP-hard under Turing reductions, but can be solved in polynomial time if 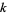 is fixed.

A related problem asks for the largest integer not representable as some linear combination of 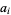s (possibly assumed to have 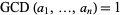) is sometimes known as the coin problem.

REFERENCES:

Guy, R. K. "The Postage Stamp Problem." §C12 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 123-127, 1994.

Hofmeister, G. "Asymptotische Aschätzungen für dreielementige extremalbasen in natürlichen Zahlen." J. reine angew. Math. 232, 77-101, 1968.

Hofmeister, G. "Die dreielementige Extremalbasen." J. reine angew. Math. 339, 207-214, 1983.

Hujter, M. and Vizvari, B. "The Exact Solutions to the Frobenius Problem with Three Variables." J. Ramanujan Math. Soc. 2, 117-143, 1987.

Mossige, S. "Algorithms for Computing the 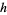-Range of the Postage Stamp Problem." Math. Comput. 36, 575-582, 1981.

Mossige, S. "On Extremal 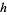-Bases 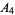." Math. Scand. 61, 5-16, 1987.

Mossige, S. "The Postage Stamp Problem: An Algorithm to Determine the 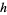-Range on the 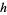-Range Formula on the Extremal Basis Problem for 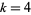." Math. Comput. 69, 325-337, 2000.

Nijenhuis, A. "A Minimal-Path Algorithm for the 'Money Changing Problem.' " Amer. Math. Monthly 86, 832-835, 1979.

Shallit, J. "The Computational Complexity of the Local Postage Stamp Problem." ACM SIGACT 33, 90-94, 2002.

Sloane, N. J. A. Sequence A014616 in "The On-Line Encyclopedia of Integer Sequences."

Stöhr, A. "Gelöste und ungelöste Fragen über Basen der natürlichen Zahlenreihe I, II." J. reine angew. Math. 194, 111-140, 1955.

 Wagon, S. "Greedy Coins." https://library.wolfram.com/infocenter/MathSource/5187/.