The Mordell conjecture states that Diophantine equations that give rise to surfaces with two or more holes have only finite many solutions in Gaussian integers with no common factors (Mordell 1922). Fermat's equation has 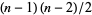 holes, so the Mordell conjecture implies that for each integer 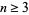, the Fermat equation has at most a finite number of solutions.

This conjecture was proved by Faltings (1984) and hence is now also known as Falting's theorem.

REFERENCES:

Bombieri, E. "The Mordell Conjecture Revisited." Ann. Scuola Norm. Sup. Pisa Cl. Sci. 17, 615-640, 1990.

Cornell, G. and Silverman, J. H. Arithmetic Geometry. New York: Springer, 1986.

Elkies, N. D. "ABC Implies Mordell." Internat. Math. Res. Not. 7, 99-109, 1991.

Faltings, G. "Endlichkeitssätze für abelsche Varietäten über Zahlkörpern." Invent. Math. 73, 349-366, 1983.

Faltings, G. "Die Vermutungen von Tate und Mordell." Jahresber. Deutsch. Math.-Verein 86, 1-13, 1984.

Hindry, M. and Silverman, J. H. Diophantine Geometry. New York: Springer, 2000.

Ireland, K. and Rosen, M. "The Mordell Conjecture." §20.3 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 340-342, 1990.

Mordell, L. J. "On the Rational Solutions of the Indeterminate Equation of the Third and Fourth Degrees." Proc. Cambridge Philos. Soc. 21, 179-192, 1922.

van Frankenhuysen, M. "The ABC Conjecture Implies Roth's Theorem and Mordell's Conjecture." Mat. Contemp. 16, 45-72, 1999.