The Markov numbers 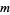 are the union of the solutions  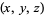to the Markov equation

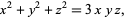(1)

and are related to Lagrange numbers 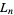 by

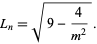(2)

The first few solutions are 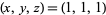, (1, 1, 2), (1, 2, 5), (1, 5, 13), (2, 5, 29), .... All solutions can be generated from the first two of these since the equation is a quadratic in each of the variables, so one integer solution leads to a second, and it turns out that all solutions (other than the first two singular ones) have distinct values of , , 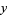and 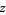, and share two of their three values with three other solutions (Guy 1994, p. 166). The Markov numbers are then given by 1, 2, 5, 13, 29, 34, ... (OEIS A002559).

The Markov numbers for triples 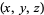 in which one term is 5 are 1, 2, 13, 29, 194, 433, ... (OEIS A030452), whose terms are given by the recurrence relation

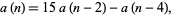(3)

with 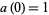, , 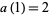, 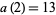and .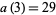

The solutions can be arranged in an infinite tree with two smaller branches on each trunk. It is not known if two different regions can have the same label. Strangely, the regions adjacent to 1 have alternate Fibonacci numbers 1, 2, 5, 13, 34, ..., and the regions adjacent to 2 have alternate Pell numbers 1, 5, 29, 169, 985, ....

Let 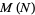 be the number of triples with 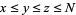, then

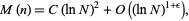(4)

where 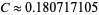 (Guy 1994, p. 166).

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 187-189, 1996.

Cusick, T. W. and Flahive, M. E. The Markov and Lagrange Spectra. Providence, RI: Amer. Math. Soc., 1989.

Descombes, R. "Problèmes d'approximation diophantienne." Enseign. Math. 6, 18-26, 1960.

Guy, R. K. "Don't Try to Solve These Problems." Amer. Math. Monthly 90, 35-41, 1983.

Guy, R. K. "Markoff Numbers." §D12 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 166-168, 1994.

Sloane, N. J. A. Sequences A002559/M1432 and A030452 in "The On-Line Encyclopedia of Integer Sequences."