There are two distinct entities both known as the Lagrange number. The more common one arises in rational approximation theory (Conway and Guy 1996), while the other refers to solutions of a particular Diophantine equation (Dörrie 1965).

Hurwitz's irrational number theorem gives the best rational approximation possible for an arbitrary irrational number 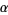 as

(1)

The 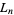 are called Lagrange numbers, and get steadily larger for each "bad" set of irrational numbers which is excluded, as indicated in the following table.

	exclude
1	none
2
3

Lagrange numbers are of the form

(2)

where 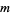 is a Markov number. The Lagrange numbers form a spectrum called the Lagrange spectrum.

Given a Pell equation (a quadratic Diophantine equation)

(3)

with 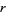 a quadratic surd, define

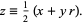(4)

for each solution with 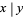. The numbers  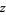are then known as Lagrange numbers (Dörrie 1965). The product and quotient of two Lagrange numbers are also Lagrange numbers. Furthermore, every Lagrange number is a power of the smallest Lagrange number with an integer exponent.

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 187-189, 1996.

Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 94-95, 1965.